(1) 歳差運動の正体
-
自転車操業とは、 倒産しそうな零細企業が赤字覚悟で操業を続けることです。 自由競争経済社会においては、 零細企業に限らず企業のあり方そのものが、 自転車操業になっています。 黒字企業であっても、 もうけ続ければならない自転車操業になっているのです。 重心が支点よりも高い位置にあって不安定になっているからこそ、 不安定の中の安定 ( 重心が支点の真上にあること ) を求め続けならなければならず、 その結果、 経済が発展していくしくみになっているのです。 そのおかげで生活が豊かになってきたのですが、 いろんなものが犠牲になっているのもまた事実で、 今後も私たちが乗り越えて行かなければならない課題となっています。
さて、 転倒とは、 重心が支点よりも高い位置にあるときに、 重心が支点よりも低い位置に向かおうとする運動のことです。 転倒の原動力となる力のモーメントの大きさは、 重心と支点との水平方向の距離に比例しますので、 重心が支点の真上にあるときは、 転倒は起こりません。 秋田竿燈まつりでは、 額で重たい竿燈を支え続ける技が披露されますが、 それは常に支点を重心の真下に持ってくるように調節し続けているのです。軸が鉛直方向から少しでも傾くと、その方向に軸を転倒しようとする力が働きます。
回転していないコマは床の上に真っ直ぐに立てようとしても手を離した直後に転倒してしまいます。 しかし、 回転しているコマは転倒しにくく、 それも回転の速度、 それは角速度で表させるのですが、 が大きいほど転倒しにくくなっています。 角速度は回転面に垂直な右ネジの進行方向になっていて、 回転速度が大きいほど長いベクトルで表されます。
コマの首振り運動は、 歳差運動と言われます。 首振り運動の回転方向はコマの回転運動の方向と同じ方向です。 歳差運動は、 コマの回転の角速度がコマの転倒の角速度を飲み込んで転倒を無くしている現象ではありません。 歳差運動は「多重ジャイロ効果による姿勢制御(私によるネーミング)」の崩壊現象です。
多重ジャイロ効果とは :
元の回転方向に対して垂直な方向に持続的に力のモーメント (トルク) が作用すると、まず、異なる方向に新たな回転が生じます ( 直接作用 ) 。なお、力の方向とトルクの方向は垂直になっています。トルクは回転中心からの位置ベクトルに力を外積させたものだからです。 次に、
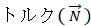 は
は 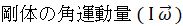 に対して、次の式で与えられる影響を及ぼします ( 間接作用と言うことにします ) 。
に対して、次の式で与えられる影響を及ぼします ( 間接作用と言うことにします ) 。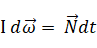
※ 左辺は 角運動量の微小変化 で、右辺は 微小トルク積 です。
つまり、このトルクは、剛体に新たな角速度を加えようと作用する( 直接作用 )だけでなく、元々の剛体の角速度そのものの方向を変えるような作用( 間接作用 )もするということです。角速度の変化の方向がトルクの方向になっていることに注目してください。その意味は後ほど具体例で示します。そしてこの間接作用は「見かけのトルク」による直接作用と見なすことができます。「見かけのトルク」の方向は元のトルクの方向と直角になっています。ここまでがジャイロ効果の原理です。
その次に、見かけのトルクによる間接作用が生じて、それは、新たな見かけのトルクによる直接作用と見なすことができます。そのまた次に、新たな見かけのトルクによる間接作用が生じて、それは、さらに新たな見かけのトルクによる直接作用と見なすことができます。こういったことが短時間に連鎖するうちに、新たに生じた回転たちは互いに打ち消しあって、元々の剛体の角速度だけが保存されるようになります。これを私は「多重ジャイロ効果による姿勢制御」と言っています。
とは言っても、実際は空気抵抗などによって元の回転が次第に衰えてくるので、元の回転の単位時間当たりの変化量が次第に少なくなっていって、見かけのトルクは次第に小さくなっていきます。したがって元の回転に他の方向の回転が合成されていき少しずつ変化していきます。
※ 自己座標系は「 左右軸 ( x 軸 ) 」「 下上軸 ( y 軸 ) 」「 後前軸 (z軸 ) 」からなる3次元直交座標系で、原点は眉間にあります。
自己座標系において y 軸の正の方向を向く回転ベクトル
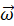 があるとします。これに対して z軸の正の方向を向くトルクを作用させ続けます。このトルクによる直接作用で新たに z軸の正の方向を向く回転が発生します。と同時に、このトルクの間接作用は、y 軸の正の方向を向く
があるとします。これに対して z軸の正の方向を向くトルクを作用させ続けます。このトルクによる直接作用で新たに z軸の正の方向を向く回転が発生します。と同時に、このトルクの間接作用は、y 軸の正の方向を向く 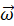 を z軸の正の方向に向けようと、
を z軸の正の方向に向けようと、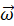 に対して yz平面上を回転させようとします。これは「見かけのトルク」による直接作用と見なすことができます。その後、トルクの間接作用の連鎖が起こって次々に「見かけのトルク」が誕生していきますが、その誕生の順に見かけのトルクの向きを示すと次のようになります。
に対して yz平面上を回転させようとします。これは「見かけのトルク」による直接作用と見なすことができます。その後、トルクの間接作用の連鎖が起こって次々に「見かけのトルク」が誕生していきますが、その誕生の順に見かけのトルクの向きを示すと次のようになります。x 軸の負の方向 → z軸の負の方向 → x 軸の正の方向 → z軸の正の方向 → x 軸の負の方向 → ・・・・
※ 子トルクの向き = 元々の剛体の角速度 に 親トルク を外積させた方向
つまり、見かけのトルクは xz平面上を90度毎に回転移動していることになります。その回転移動の向きは、元の回転ベクトルと同じ y 軸の正の方向を向いています。
とは言っても、実際は空気抵抗などによって元の回転が次第に衰えてくるので、元の回転の単位時間当たりの変化量が次第に少なくなっていって、見かけのトルクは次第に小さくなっていきます。したがって元の回転に他の方向の回転が合成されていき少しずつ変化していきます。これがコマの歳差運動の正体です。
-
重力加速度: g m/s2
コマの質量: m kg
コマの軸を回転軸とする慣性モーメント: I kgm2
コマの重心の軸先からの位置ベクトル:
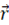
コマの重心の軸先からの距離: r m
角速度
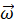 ( 大きさ ω rad/s )で回転しているコマを横から一瞬水平方向に力を加えて転倒させとうとすると、回転の角速度の大きさは変化せず、角速度の方向が垂直方向から θ rad だけ傾いた。その後1分間は角速度の大きさ ω rad/s と コマの傾き θ rad は一定で、コマは歳差運動を行った。このときの歳差運動の角速度の大きさを Ω rad/s とすると、Ω は g と m と I と r と
( 大きさ ω rad/s )で回転しているコマを横から一瞬水平方向に力を加えて転倒させとうとすると、回転の角速度の大きさは変化せず、角速度の方向が垂直方向から θ rad だけ傾いた。その後1分間は角速度の大きさ ω rad/s と コマの傾き θ rad は一定で、コマは歳差運動を行った。このときの歳差運動の角速度の大きさを Ω rad/s とすると、Ω は g と m と I と r と 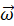 と θ を用いてどのように表されるだろうか?
と θ を用いてどのように表されるだろうか?
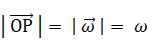
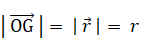
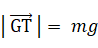
回転軸の支点: О
コマの重心: G
重力によるコマの転倒トルク:
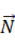 向きは、画面の手前から奥へと向かう方向
向きは、画面の手前から奥へと向かう方向大きさは、 N = mgrsinθ kgm/s2 ・・・ ②
コマの角運動量:
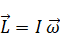 大きさは、 Iω kgm2rad/s
大きさは、 Iω kgm2rad/s回転運動方程式:
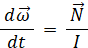
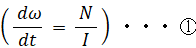
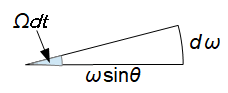
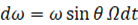 ・・・ ③
・・・ ③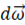 の向きは、重力によるコマの転倒トルクの向きと同じ
の向きは、重力によるコマの転倒トルクの向きと同じ② と ③ を ① に代入して、
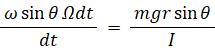
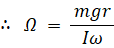
<
 剛体力学 へ戻る
剛体力学 へ戻る