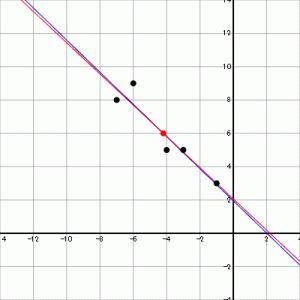
２次元直交座標系に散在する点たちの重心を通り、 回帰直線に近い直線で、 それぞれの点からその直線への距離の総和が最小になっている。 そんな直線を 「 最小２乗直線 」 と呼ぶことにしよう。
　 回帰直線とは、 ２次元直交座標系に散在する点たちの重心を通り、 それぞれの点からその直線への y 軸方向の距離の総和が最小になっている、 そんな直線である。


Data = [ [−1,3], [−3,5], [−4,5], [−6,9], [−7,8] ]
このときの 回帰直線 と 最小二乗直線 を求めるプログラムを示す。

　　　　　　　　　　　　　− 回帰直線　　　− 最小２乗直線
　　　　　　


　 最小２乗直線の近似を求める方法に、 「 分散共分散行列 」 の固有ベクトルを利用する方法がある。 x の分散は 4.56 、 y の分散は 4.8 、 x と y の共分散は 4.4　なので、 分散共分散行列は次のようになる。
　　　　　
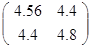
　 ２つの直交する固有ベクトルのうち回帰直線に近い方は、 固有値 ＝ 0.27836394053302 に対応する固有ベクトルである。
この固有ベクトルの傾きは最小２乗直線の傾きに近似する。
固有ベクトルは、
　　　　私が作成した十進BASIC のプログラムでは、 ( 0.716680748373205, −0.697401394400113 ) になり、
　　　　Maximaでは、 ( 1, −(sqrt(12109)-3)/110 ) になる。
したがって、 固有ベクトルの傾きは次のようになる。
　　−0.697401394400113　÷　0.716680748373205　＝　−(sqrt(12109)-3)/110　≒　−0.973099104424314
最小２乗直線は点たちの重心 （ −4.2,　6 ） を通るので、 この直線の方程式が得られる。
こうして求められた最小２乗直線に近似した直線の全ての点からの距離の合計は、 2.19312575413418 となって、 このケースでは回帰直線のそれ 2.17148177998712 よりも大きくなってしまう。