数字を逆さに並べて元の数に加えると 333333 になる数はいくつあるでしょうか？

　 条件を満たす数は 333333 以下であることは明らかです。 また、 ５桁の数字 99999 を逆さに並べて元の数字に加えても 333333 には届きませんので、 ６桁の数字であることも解ります。 したがって、 条件を満たす数の10万の位の数は１〜３のどれかであると言えます。 したがって、 条件を満たす数の１の位の数は０〜３のどれかであり、 加えたときに１の位では繰上げがないことも解ります。

　 加えたときにどの位でも繰り上げのない場合について考えてみましょう。 10万の位の数は１〜３のどれかです。 10万の位の数字が決まれば、 １の位の数字が１つだけ決まります。 １万の位の数は０〜３のどれかです。 １万の位の数字が決まれば、 十の位の数字が１つだけ決まります。 千の位の数は０〜３のどれかです。 千の位の数字が決まれば、 百の位の数字が１つだけ決まります。 したがって、 場合の数は次のようになります。
　　　　　

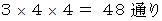
　 さて、 加えたときに、 10万の位と１の位の数字は等しいこと、 かつ、 １万の位と十の位の数字は等しいこと、 かつ、 千の位の数字と百の位の数字は等しいこと。 これが数字を逆さに並べて元の数に加えると 333333 になるための必要条件です。
　 ここで、 加えたときに１万の位と十の位のみで繰り上げがある場合について考えてみましょう。 この場合は、 加えたときに千の位の数よりも百の位の数の方が１つ大きくなりますので、 千の位の数字と百の位の数字は等しいことという必要条件に当てはまりません。
　 次に、 加えたときに千の位と百の位のみで繰り上げがある場合を考えてみましょう。 この場合は、 加えたときに百の位の数よりも千の位の数の方が１つ大きくなりますので、 千の位の数字と百の位の数字は等しいことという必要条件に当てはまりません。
　 その次に、 加えたときに、 10万の位と１の位以外の全ての位で繰り上げがある場合について考えてみましょう。 この場合は、 加えたときに１の位の数よりも10万の位の数が１つ大きくなりますので、 10万の位と１の位の数字は等しいことという必要条件に当てはまりません。
　 以上の考察より、 加えたときに繰上げが生じないことが、 数字を逆さに並べて元の数に加えると 333333 になるための必要条件であることが解りました。 したがって、 加えたときに繰り上げのない場合の数がそのまま答えになっていることが解ります。


　 この問題を解くプログラムを４つ作ってみました。