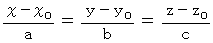例題1 :
点( −7,0,4 )と 点( 0,14,11 )を結ぶ直線の方程式を求めよ
( 解答 )
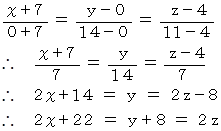
例題2 :
点( 1,−2,−6 )を通り、 ベクトル( −1,1,−1 )に垂直な平面A がある。
点( −2,−2,1 )を通り、 ベクトル( 1,−2,3 )に垂直な平面B がある。
この2つの平面の交わる直線の方程式を求めよ。
( 解答 )
平面A の方程式 : −1×( x−1 )+ 1×( y+2)− 1×( z+6 ) = 0
つまり、 −x+y − z = 3 ・ ・ ・ ・

平面B の方程式 : 1×( x+2 )− 2×( y+2 )+ 3×( z−1 )= 0
つまり、 x−2y+3z = 5 ・ ・ ・ ・

 と
と  を 辺々加えて、 y = 2z−8
を 辺々加えて、 y = 2z−8 の 辺々 に2をかけたもの と
の 辺々 に2をかけたもの と  を 辺々加えて、 x = z−11
を 辺々加えて、 x = z−11z = t と置くと、 求める直線の媒介表示 は次のようになる。
( x,y,z ) = ( −11+t,−8+2t,0+t )
したがって、 この直線の方程式は次のようになる。
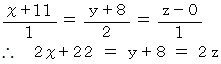
 ベクトル解析 へ戻る
ベクトル解析 へ戻る