三角形の重心とは、 一様な重力場に垂直に三角形を位置取りさせて、 ある一点に重力場と反対向きの力を作用させたときに、 三角形に作用する力のモーメントがゼロになる点のことです。 三角形のそれぞれの頂点と対辺の中点を線分で結んだときにできる交点は、 その三角形の重心と一致します。 そこで、 三角形の重心とはそういう定義であると数学的理解で終わらせてしまっている人がほとんどです。 今日は、 そこをもう一つ深く掘り下げて、 三角形の重心の物理学的理解へと迫ります。
実験:
一様な厚紙で三角定規と同じくらいの大きさの三角形を作り、 3辺すべてに6等分する点を打っておきます。 三角形の1面には、 それぞれの頂点と対辺の中点を結ぶ線分を描きます。 三角形のもう一つの面には、 それぞれの辺に平行で三角形の高さの3分の1および3分の2に位置する直線を描きます。
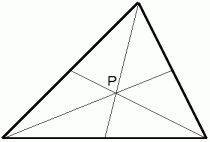
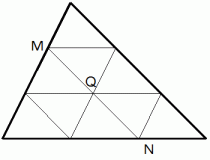
三角定規の一番とんがった角の上に点P を乗せて三角形が落ちないようにバランスをとってください。 うまくいったら、 今度は点Q を乗せてやってみてください。 それがうまくいったら、 次は、 定規の辺の上に線分
 を乗せてバランスをとってください。
を乗せてバランスをとってください。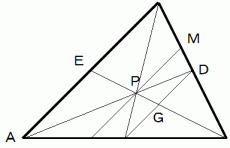
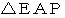 と
と 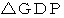 は大きさが
は大きさが 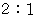 の相似になっています。
の相似になっています。それは、 中点連結定理を用いて証明することができます。
以上の実験が三角形の重心の物理学的理解へのヒントになります。
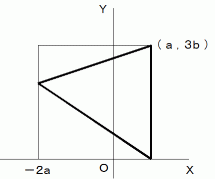
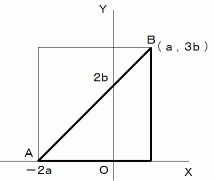
上の左図の三角形において、辺上の同じ x 座標値 を持つ2つの点を結ぶ線分の長さにY軸からの距離をかけた値の総計がY軸の左右で等しくなっているはずです。 なぜならば、Y軸にかかる力のモーメント
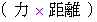 がゼロになっているからです。 また、 左図の線分の長さは、 右図のような面積の等しい直角三角形の線分の長さに等しくなっています。 辺
がゼロになっているからです。 また、 左図の線分の長さは、 右図のような面積の等しい直角三角形の線分の長さに等しくなっています。 辺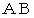 を含む直線の方程式は、 次のようになります。
を含む直線の方程式は、 次のようになります。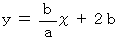
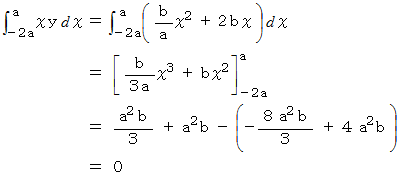
この式より、 Y軸にかかる力のモーメントがゼロになっていることが確かめられました。
三角形の重心が理解できれば、 四角形の重心もすぐに解ります。 四角形を4つの三角形に分割し、 4つの三角形の重心で作る系の重心を求めます。 それは平行四辺形
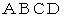 の対角線の交点になります。
の対角線の交点になります。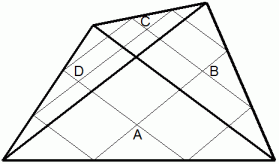
参照: ベクトル解析 > 三角形の重心の位置ベクトル
 解析学 へ戻る
解析学 へ戻る