（ 問 題 ）

　 円周上に任意に３点をとり、 この３点を線分で結んで三角形を作る。 このとき鋭角三角形になる確率を求めよ。

（ 解 答 ）

　 厳密にいうと直角三角形になる確率はゼロですから、 鋭角三角形になる確率は、 １ から鈍角三角形になる確率を引いたものになります。 そこで、 まず鈍角三角形になる確率を求めます。
　 最初の１点はどこにとっても同じですから、 その後に２点をとる場合に鈍角三角形になる確率を求めればいいのです。 円周の長さを10とします。 そういう輪になったひもを頭の中に用意してください。最初の１点をとったら、 その点にハサミを入れ、 一本のひもにします。 この長さ10の直線分に任意の２点をとったとき、 鋭角三角形になるための必要十分条件は、 次の または を満たすことになります。
　　　　 ２点が直線分の中点を境にして左右のどちらかに偏在すること
　　　　 ２点が直線分の中点を境にして左右に分かれて存在していて、
　　　　　　かつ、 ２点間の距離が５よりも大きいこと

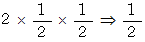
　 の確率 ：
　　　　　　
　の確率 ：
　　　　２点が直線分の中点を境にして左右のどちらかに偏在していなくて、かつ、２点の近い方
　　　の端までの距離の和が５よりも小さいことと同じですから、 次のようになります
　　　　　　　
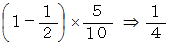
したがって、 鈍角三角形になる確率は次のようになります。
　　　　　　
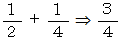
したがって、 鋭角三角形になる確率は次のようになります。
　　　　　　

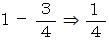
では、 十進BASIC のプログラムでシミュレーションしてみましょう。