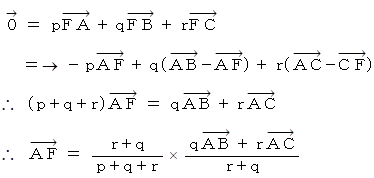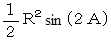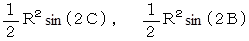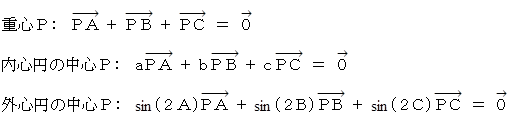三角形の心から頂点へ
 ベクトル解析 へ戻る
ベクトル解析 へ戻る
 大学生のための数学 へ戻る
大学生のための数学 へ戻る
2019.02.23____
三角形ABCがあります。 次のようにします。
頂点Aの内角の大きさを A
頂点Bの内角の大きさを B
頂点Cの内角の大きさを C
頂点Aの対辺BCの長さを a
頂点Bの対辺CAの長さを b
頂点Cの対辺ABの長さを c
辺BC上に点Dをとります。 BD : DC = r : q とします。
線分AD上に点Pをとります。
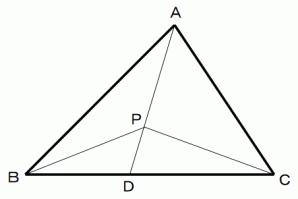
(1) △ABP と △ACP の面積の比は r : q であることを示してください。
△ABD と △ACD の面積の比は r : q である。 なぜならば、 高さが等しいので。
△PBD と △PCD の面積の比は r : q である。 なぜならば、 高さが等しいので。
△ABPの面積は、 △ABDの面積から△PBDの面積を引いたものである。
△ACPの面積は、 △ACDの面積から△PCDの面積を引いたものである。
したがって、△ABP と △ACP の面積の比は r : q である。
(2) 三角形ABCの中に点Fを取ります。
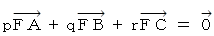 のとき、 △ABF と △ACF の面積の比は r : q であることを示してください。
のとき、 △ABF と △ACF の面積の比は r : q であることを示してください。
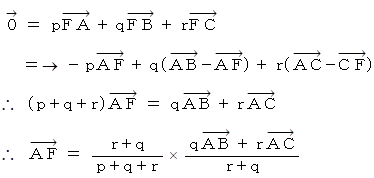
この式より、 Fは頂点Aと辺BCを r :q の比に内分する点とを結ぶ線分上にあることが判る。
したがって、 (1)より、 △ABF と △ACF の面積の比は r : q であることが判る。
(3) 三角形の重心を点Pとします。
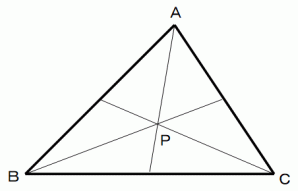
△ABP と △PBC と △ACP の面積は等しいことを示してください。
重心はそれぞれの頂点と対辺の中点とを結ぶ線分が交わる点である。
(1)より、 △ABP と △PBC と △ACP の面積は等しいことが判る。
(4) 三角形の内心円の中心を点Pとします。
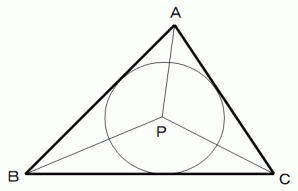
△ABP と △PBC と △ACP の面積の比は、c : a : b であることを示してください。
すべて高さが等しいので、 面積の比は、c : a : b である。
(5) 三角形の外心円の中心を点Pとします。
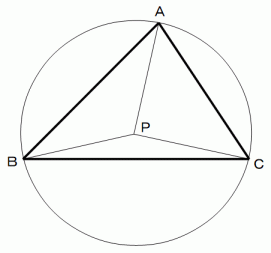
△ABP と △PBC と △ACP の面積の比は、sin(2C) : sin(2A) : sin(2B) であることを示してください。
円周角の定理より、 ∠BPCは∠BACの2倍である。
外心円の半径をRとすると、 △PBCの面積は次のようになる。
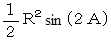
同様にして、 △ABP と △ACP の 面積はそれぞれ次のようになる。
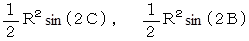
したがって、 △ABP と △PBC と △ACP の面積の比は、 sin(2C) : sin(2A) : sin(2B) である。
(6)結論
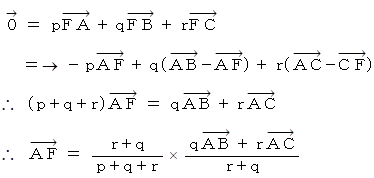
 ベクトル解析 へ戻る
ベクトル解析 へ戻る 大学生のための数学 へ戻る
大学生のための数学 へ戻る
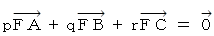 のとき、 △ABF と △ACF の面積の比は r : q であることを示してください。
のとき、 △ABF と △ACF の面積の比は r : q であることを示してください。