（１） ３点を通る放物線と円の方程式

　 ３点を通る放物線と円の方程式を求めてみましょう。
　 放物線の場合は 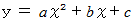、 円の場合は 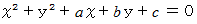に と の３ペアの値を代入して得られる 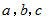についての３つの方程式を、 連立３元一次方程式として解きます。 たとえば、 ３点 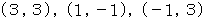を通る放物線の方程式は、 次の連立３元一次方程式を解くことになります。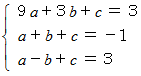
　　　　　
　 これを解くと、 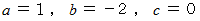になりますので、 求める放物線の方程式は次のようになります。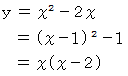
　　　　　
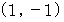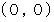　 この方程式を見ますと、 この放物線は、 頂点を とする下に凸の方程式で、 軸とは 点 と 点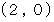 で交わることがわかります。

　 十進BASIC で、 ３点を通る放物線と円の方程式を表示するプログラムを作ってみました。


　　　　　　　　　　　　　　　　　　

（２） ３点を結んでできる三角形の外接円の方程式

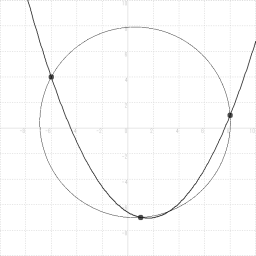
問 題 ：
　　　　　点Ａ（ ５，−３ ）　　　点Ｂ（ −２，４ ）　　　点Ｃ（ ７，１ ）　がある。
　　　　　以上の３つの点を結んでできる三角形の外接円の方程式を求めなさい。


解 答 ：

　 点Ａ と 点Ｂ を結ぶ線分の垂直二等分線　と　点Ｂ と 点Ｃ を結ぶ線分の垂直二等分線　との交点が外接円の中心だから ・ ・ ・ ・　という方法で答えを求めようとすると苦労する。
　 この問題は、 点Ａ と点Ｂと点Ｃを通る円の方程式を求めなさいという問題であるので、 次の円の方程式に と の３ペアの値を代入していって、 連立３元一次方程式を作って解けばよい。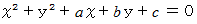
　　　　　
成立する連立３元一次連立方程式
　　
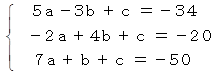
これを解くと、
　　　　
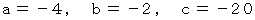
したがって、 求める外接円の方程式は次のようになる。
　　　　
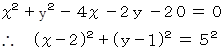
したがって、 求める外接円は 中心（ ２，１ ） 半径５ の円であることが解った。


　 十進BASIC で、 連立３元一次方程式の解を求めるプログラムを作ってみました。