成功確率が Ｐ であるトライを ｎ 回試行したときの成功回数の期待値はいくらだろうか？
　 １ 回の試行における成功回数の期待値は Ｐ だから、 ｎ 回試行すれば ｎＰ 回成功するだろうと期待できる。そのとうりだ。

　 一方、 ｎ 回試行したときに ｋ 回成功する確率は
　　　　
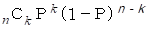
である。　だから、 次の式が成り立つ。
　　　　


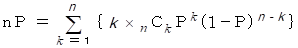
　 次のような十進BASIC の プログラムで確かめてみた。
　　　　LET P = 2/3
　　　　LET n = 9
　　　　LET COUNT = 0
　　　　FOR i=0 TO n
　　　　　　LET COUNT = COUNT + i * COMB(n,i) * P^I * (1-P)^(n-i)
　　　　NEXT i
　　　　PRINT COUNT
　　　　PRINT n * P
　　　　END


＜シミュレーション＞

10分の1の確率で当たりが出るくじがあります。引いたくじは元に戻します。
10回くじをひいて何回当たるでしょうか？ 10万回試行します。

　　　



　１回も当たらない確率は、
　　　　
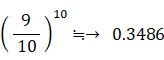
　これの近似値を求めてみる。10回を単位時間と考えて、単位時間当たり１回イベントが生ずるとする。イベントが発生した直後から単位時間が経過するまでに次のイベントが発生する確率は、指数分布の累積分布より 1−1/e ( e はネイピア数 )。 ということは、イベントが発生した直後から単位時間が経過するまでに次のイベントが発生しない確率は、1/e ≒ 0.3679。 ちなみに、1/e になるのは、当たりの確率 1/n の独立試行を n 回行ってもハズレばかりだった場合の n が無限大のときである。
　　　※ 参照：　数理論 ＞ ネイピア数にまつわる問題

プログラムの内容 ：