（１） スカラー場の面積分

　 スカラー場の面積分とは、曲面上の全ての点に与えられている数の総和のことです。

　 スカラー場 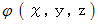の中に 曲面 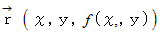があるとき、 この曲面上のスカラー 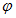の積分を面積分といい、 次のように表されます。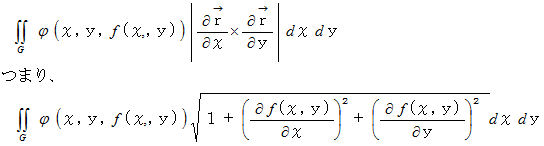
　　　　

　 この式と曲面の面積の式とを比べて見てください。 曲面の面積の式 は、 次の様なスカラー場内でのスカラー 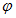の面積分になっていることが解ります。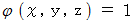
　　　　

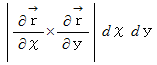　 は、 ＸＹ平面上に投影された曲面の微小区分の面積 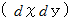に対応する実際の曲面の区分された微小区間の面積を表しています。 これは面積素と言われます。 面積素に法線向きの方向性を付加したものは、 ベクトル面積素と言われ、 次の式で表されます。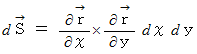
　　　　
曲面の単位法ベクトル 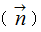は次のように表されます。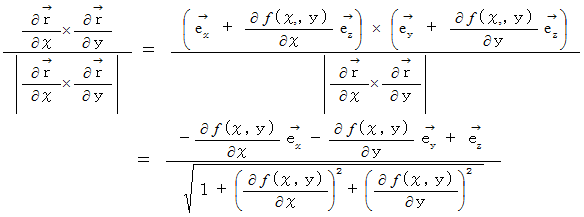
　　　　
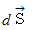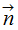と には次のような関係があります。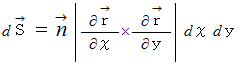
　　　　

（２） ベクトル場の面積分

　 ベクトル場の面積分とは、 曲面上の全ての点に与えられているベクトルとその点のベクトル面積素との内積の総和のことです。 したがって、 ベクトル場を面積分して得られるものは、 ベクトルではなくてスカラーです。 曲面に垂直な方向にどれだけの流体の流れ（ 流束 ）があるのかを調べるときなどに用いられています。

　 ベクトル場 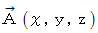の中に 曲面 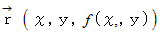があるとき、 この曲面上のベクトル場 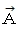と ベクトル面積 との内積の総和を面積分といい、 次のように表されます。
　　　　
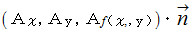　 はスカラーですから、 面積分とは、 曲面上のベクトル 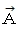の曲面と垂直な成分の大きさの総和 （ スカラー場の面積分 ） であることが解ります。
（ 面積分には、 これ以外にも外積型がありますが、 ここでは触れません。）



例題 ：　 ベクトル場 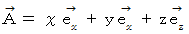の中に次のような曲面があるとき、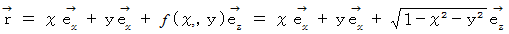
　　　　　　　　
　　　 　ベクトル をこの曲面全体にわたって面積分しなさい。

（ 答 え ）
　　　
　　　
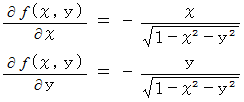
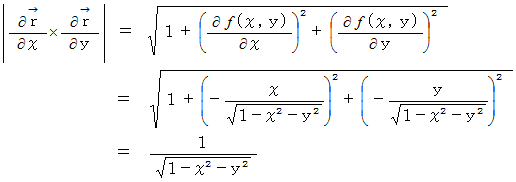
　　　したがって、
　　　
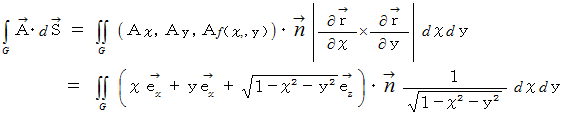
　　　ベクトル 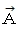は常にこの曲面に対して垂直なので、 次のようになる。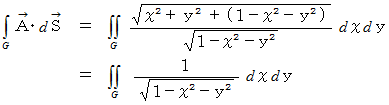
　　　　　
　　　　　ここで、 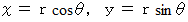と置くと、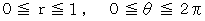

　　　　　　　　
　　　　　　　　
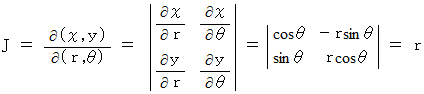
　　　　　したがって、
　　　　　
　　　　　

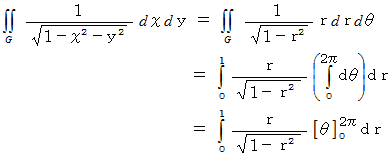
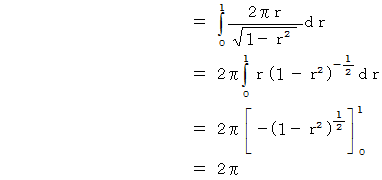
ちなみに、球の表面積の公式は 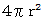です。