曲線　y ＝ f ( x )　の　( k , f ( k ) )　における傾きは　f ' ( k )　になります。ただし、 f ' ( k )　は次の式によります。
　　　
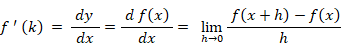
　傾き（ ２次元平面での勾配 ）を求めるのが 微分 であり、それは次の式で表されます。
　　　

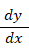
　一方、積分 といえば、グラフでいうと、曲線　y ＝ f ( x )　と ３つの直線 (　y ＝ 0　と　x ＝ a　と　x ＝ b　) で囲まれる部分の面積というイメージがあります。積分は次のように表されます。
　　　
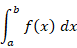
　y dx つまり f ( x ) dx は　曲線　y ＝ f ( x )　と　直線　y ＝ 0　とで挟まれる微小な幅の長方形の面積であり、それを区間　a ≦ x ≦ b　で合計したものというイメージです。

　以上の積分のイメージは高等数学を身に着けた人にとっての話であって、微分・積分の初心者には少し早すぎるのです。なぜなら、元来「 積分とは、微分すれば関数 f ( x ) になる関数のことである。」と定義されるからです。微分すれば関数 f ( x ) になる関数は次のように表されます。
　　　

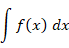
　では、なんで積分がグラフの面積を表すことになるのでしょうか？　曲線　y ＝ f ( x )　と ３つの直線 (　y ＝ 0　と　x ＝ 0　と　x ＝ b　) で囲まれる部分の面積を S ( b ) で表すことにします。まず、 0 ≦ t ≦ b−h という条件とします。すると次の式が成り立ちます。
　　　
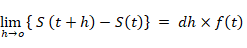
　　したがって、
　　　
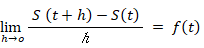
　　したがって、
　　　
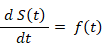
　　したがって、
　　　

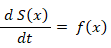
　というわけで、 f ( x ) の積分は S ( x ) であることが分かりました。ということは、S ( b ) は次のように表されるということです。