(1) スカラー場の線積分
-
スカラー場の線積分とは、 曲線上の全ての点に与えられているスカラー と その点における微小道のり との積の総和のことです。
3次元スカラー場
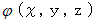 の中に曲線
の中に曲線 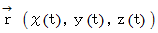 があるとき、 この曲線に沿ったスカラー
があるとき、 この曲線に沿ったスカラー 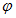 の積分を線積分といい、 次のように表します。
の積分を線積分といい、 次のように表します。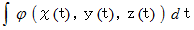
上記の式で、 時間 (
 ) のパラメーターの代りに次の弧長を用いると、 スカラー
) のパラメーターの代りに次の弧長を用いると、 スカラー 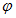 の線積分は次のようになります。
の線積分は次のようになります。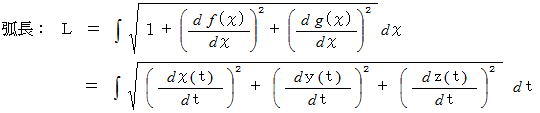
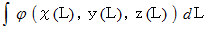
例題 : 2次元スカラー場
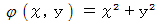 の中に次の曲線が存在します。
の中に次の曲線が存在します。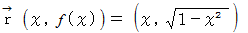
スカラー
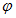 を
を 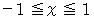 の範囲でこの曲線に沿って線積分しなさい。
の範囲でこの曲線に沿って線積分しなさい。( 答 え )
この曲線は、 中心が原点にあって、 半径
 の円の
の円の 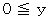 の部分の弧を表しています。 この弧を
の部分の弧を表しています。 この弧を 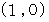 から出発して積分していくことにします。 原点と弧上の点を結ぶ線分のX軸となす角度を
から出発して積分していくことにします。 原点と弧上の点を結ぶ線分のX軸となす角度を  としますと、
としますと、  は弧長に等しくなっています。 したがって、 弧の曲線は次のように表すことができます。
は弧長に等しくなっています。 したがって、 弧の曲線は次のように表すことができます。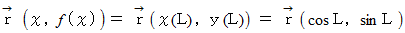
また、
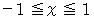 での弧の長さは
での弧の長さは 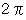 です。
です。したがって、
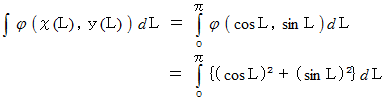
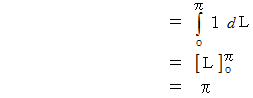
今は弧長にこだわって解答しましたが、 なにも弧長にこだわることはありません。 角度
 をパラメーターにしてもかまいません。 このとき、
をパラメーターにしてもかまいません。 このとき、  の範囲は、
の範囲は、 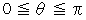 になります。
になります。高さ
 のカーテンが半径
のカーテンが半径  の円の円周に沿って立てられていときのカーテンの面積は
の円の円周に沿って立てられていときのカーテンの面積は 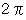 です。 2次元平面のスカラー場の線積分はこのようなイメージなのです。 しかし、 これが3次元空間のスカラー場になりますと、 ちょっとイメージしにくくなります。 それについては、 解析学 > 線積分のイメージ をご覧ください。
です。 2次元平面のスカラー場の線積分はこのようなイメージなのです。 しかし、 これが3次元空間のスカラー場になりますと、 ちょっとイメージしにくくなります。 それについては、 解析学 > 線積分のイメージ をご覧ください。-
ベクトル場の線積分とは、 曲線上の全ての点に与えられているベクトル と その点における曲線の単位接ベクトル との内積の総和のことです。 たとえば、物質にした仕事を求めるときに用います。
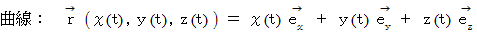 の単位接ベクトルは次のように表されます。
の単位接ベクトルは次のように表されます。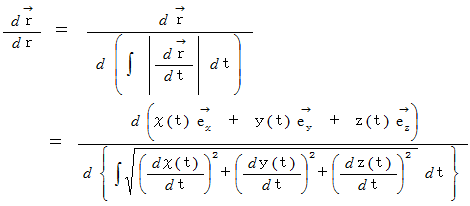
ここで、 パラメーターを時間 (
 ) から弧長 (
) から弧長 (  ) に変換します。 すると次のようになります。
) に変換します。 すると次のようになります。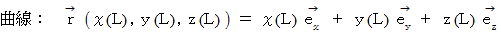
単位接ベクトル :
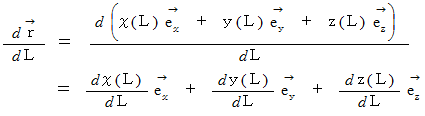
次のようなベクトル場の中に、 上の曲線があります。
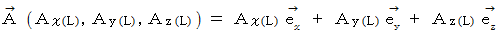
ベクトル場の線積分は次のようになります。
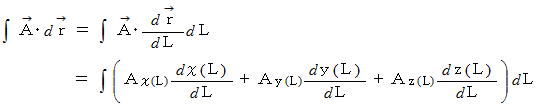
例題 : 2次元ベクトル場
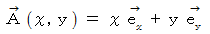 の中に次の曲線が存在します。
の中に次の曲線が存在します。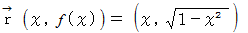
ベクトル場
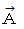 を
を 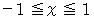 の範囲でこの曲線に沿って線積分しなさい。
の範囲でこの曲線に沿って線積分しなさい。( 答 え )
この曲線は、 中心が原点にあって、 半径
 の円の
の円の 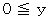 の部分の弧を表しています。 この弧を
の部分の弧を表しています。 この弧を 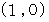 から出発して積分していくことにします。 原点と弧上の点を結ぶ線分の x 軸となす角度を
から出発して積分していくことにします。 原点と弧上の点を結ぶ線分の x 軸となす角度を  としますと、
としますと、  は弧長に等しくなっています。 したがって、 この曲線は次のように表すことができます。
は弧長に等しくなっています。 したがって、 この曲線は次のように表すことができます。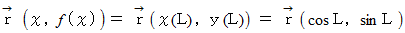
また、 この曲線の単位接ベクトルは次のようになります。
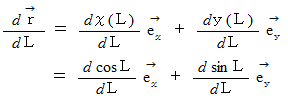
また、
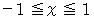 での弧の長さは
での弧の長さは  です。
です。したがって、
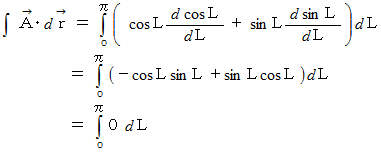
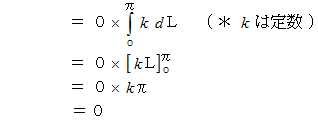
 ベクトル解析 へ戻る
ベクトル解析 へ戻る