次のような5つのベクトルがあります。
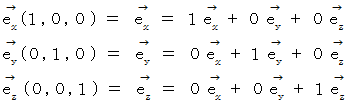
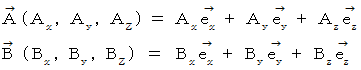
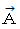 に
に 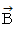 を外積させる演算 (
を外積させる演算 ( 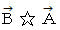 ) は、 次のように表されます。
) は、 次のように表されます。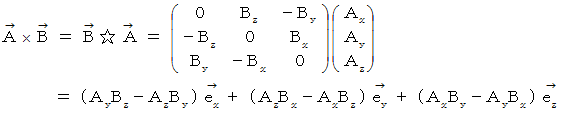
互いに直交し合っている大きさが
 の基底ベクトルたちには、 次のような関係があります。
の基底ベクトルたちには、 次のような関係があります。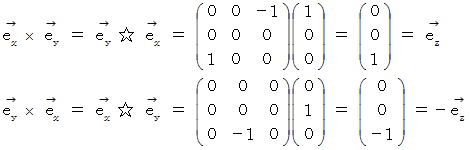
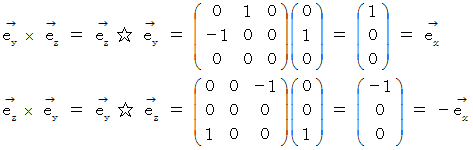
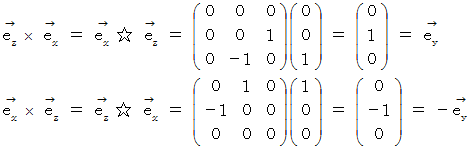
私は、 このような関係を 「 右ネジの関係 」 と言っています。 例えば
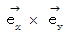 は、
は、 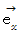 と
と  の交点を回転軸として、
の交点を回転軸として、 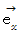 を
を  に重ねるように回転させるのを、 Z軸のプラスの方向から観察したときに、 回転の方向が反時計回りになるから、 向こうからこっちに向かって真っすぐな方向である
に重ねるように回転させるのを、 Z軸のプラスの方向から観察したときに、 回転の方向が反時計回りになるから、 向こうからこっちに向かって真っすぐな方向である 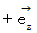 になり、
になり、 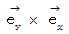 は、
は、  と
と 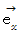 の交点を回転軸として、
の交点を回転軸として、  を
を 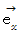 に重ねるように回転させるのを、 Z軸のプラスの方向から観察したときに、 回転の方向が時計回りになるから、 こっちから向こうに向かって真っすぐな方向である
に重ねるように回転させるのを、 Z軸のプラスの方向から観察したときに、 回転の方向が時計回りになるから、 こっちから向こうに向かって真っすぐな方向である 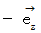 になり、
になり、  は、
は、  と
と  の交点を回転軸として、
の交点を回転軸として、  を
を  に重ねるように回転させるのを、 X軸のプラスの方向から観察したときに、 回転の方向が反時計回りになるから、 向こうからこっちに向かって真っすぐな方向である
に重ねるように回転させるのを、 X軸のプラスの方向から観察したときに、 回転の方向が反時計回りになるから、 向こうからこっちに向かって真っすぐな方向である 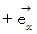 になります。
になります。もう一度、
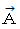 に
に 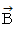 を外積させる演算 (
を外積させる演算 ( 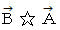 ) を見てください。
) を見てください。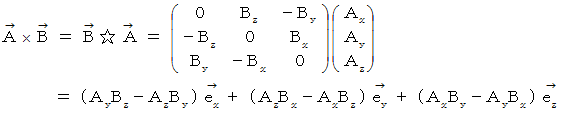
そして、
 の成分に注目してください。
の成分に注目してください。 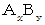 の符号は
の符号は 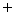 で、
で、  の符号は
の符号は 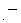 です。 ここで、 先ほどの 「 右ネジの関係 」 を思い出してください。 次の式たちが成り立っていました。
です。 ここで、 先ほどの 「 右ネジの関係 」 を思い出してください。 次の式たちが成り立っていました。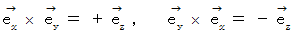
これらは似ています。 同じではありませんが似ています。
これで、 外積が簡単にできるようになったはずです。 では例題をやってみましょう。
例題 :
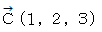 に
に 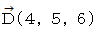 を外積させると、 どんなベクトルになるでしょうか?
を外積させると、 どんなベクトルになるでしょうか?( 答え : その1 )
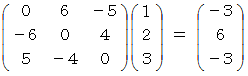
( 答え : その2 )
1 4
2 5
3 6
1 4
2 5
答えは、( 2×6−5×3,3×4−6×1,1×5−4×2 ) =→ (−3, 6, −3 )
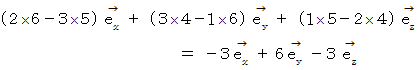
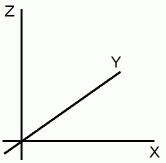
※ 一般的な3次元ベクトルの外積の求め方:
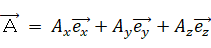
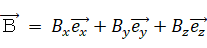
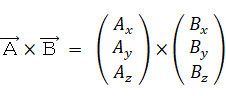
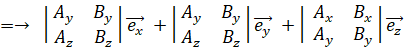
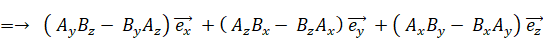
< 3次元ベクトルの外積 >
( 1/5, 2, -3 ) というベクトルの入力方法 : 1/5, 2, -3
プログラムの内容
 線形代数学 へ戻る
線形代数学 へ戻る