(1) 完全弾性衝突の試験問題の典型
-
左側から等速直線運動してきた物質A と 右側から等速直線運動してきた物質B とが、 完全弾性正面衝突をして反対方向に弾き飛びました。
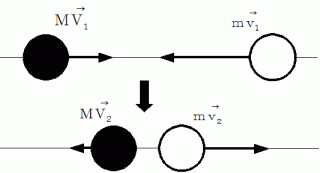
運動量保存の法則より、
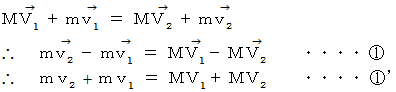
完全弾性衝突では、 エネルギー保存法則が成り立つので、
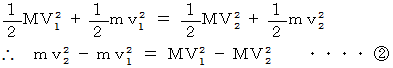
完全弾性正面衝突の試験問題の典型は、 2つの物質の質量や衝突前の速さの値が与えられ、
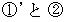 から衝突後の2つの物質の速さを求めるものです。 たとえば、 質量の等しい物質で、 衝突前の物質A と 物質B の速さがそれぞれ
から衝突後の2つの物質の速さを求めるものです。 たとえば、 質量の等しい物質で、 衝突前の物質A と 物質B の速さがそれぞれ  で与えられている場合は、 次の連立方程式を解くことになります。
で与えられている場合は、 次の連立方程式を解くことになります。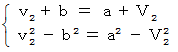
答えは、
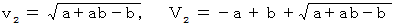 です。
です。-
完全弾性衝突ではない一般の塑性変形を生じない正面衝突においては、 2つの物質が衝突すると、 両方の物質が力を作用させ合いながら、 程度の差はありますが弾性変形がおこり、 それがまた元に戻って、 2つの物質は離れていきます。 この2つの物質が接触している短い時間を
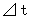 とし、 その間に物質A は物質B に対して同じ大きさ
とし、 その間に物質A は物質B に対して同じ大きさ  の力
の力  を作用するものとします。 すると、 作用反作用の法則によって、 この間に物質B が物質A に対して作用する力は
を作用するものとします。 すると、 作用反作用の法則によって、 この間に物質B が物質A に対して作用する力は  になります。力を時間で積分したものは力積と言われ、次の式が成り立ちます。
になります。力を時間で積分したものは力積と言われ、次の式が成り立ちます。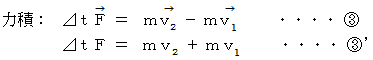
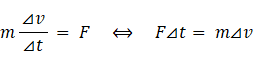
-
力積の試験問題の典型は、 物質の質量と衝突前と衝突後の速度と接触時間が与えられて、 力を求めるものです。
( 例 題 )
-
ピッチャーが投げた質量
 の ボールが 速さ
の ボールが 速さ  で水平方向に等速直線運動したとする。 これをバッターが打ったときに、 ボールは初速
で水平方向に等速直線運動したとする。 これをバッターが打ったときに、 ボールは初速  で真上に跳ね上がった。 そのときのボールとバットの接触時間を
で真上に跳ね上がった。 そのときのボールとバットの接触時間を 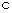 とし、接触中はボールに同じ大きさの力が作用していたものとすれば、 その力の大きさはいくらか?
とし、接触中はボールに同じ大きさの力が作用していたものとすれば、 その力の大きさはいくらか?力積 や 運動量 はベクトルですから、ベクトルの差をとらなければなりません。
答えは、
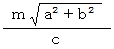

-
式
 と 式
と 式 の共通点に注目してください。
の共通点に注目してください。 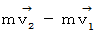 というところで、 これは衝突の前後での物質の運動量の変化を表しています。
というところで、 これは衝突の前後での物質の運動量の変化を表しています。それには理由があります。 力積は、 作用反作用の法則により、 物質A については次のようになります。
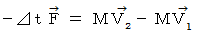
したがって、
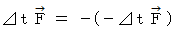 より、
より、
となり、 式
 が導かれます。
が導かれます。このことから、 運動力保存の法則とは作用反作用の法則の力積バージョンであることがわかります。
 力学 へ戻る
力学 へ戻る