数学と物理学 へ戻る図−Ａ （ 水平断面 ） 図−Ｂ （ 鉛直断面 ）
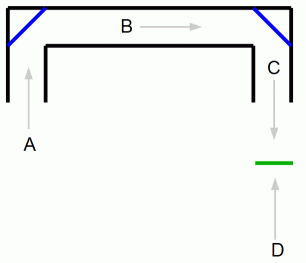
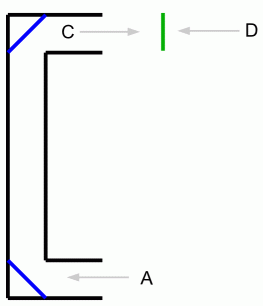
上の図は、 コの字型をした四角い潜望鏡の断面図です。 青色は鏡を表しています。 緑の透明な板にはＣ の位置から見て 上 という文字が書かれています。
図−１ 図−２
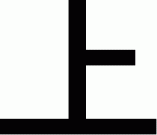
図−３ 図−４
図−１ を左右反転すると 図−２ になる。
図−１ を上下反転すると 図−３ になる。
図−１ を 180°回転すると 図−４ になる。
まず、 図−Ａ を見てください。 潜望鏡は水平に置かれています。 Ｂ の位置から見ると 図−２ になり、 Ａ の位置から見ると 図−１ になります。 水平に置かれた潜望鏡は、 インプットされた図（ Ｄの位置から見た上の字 ＝ 図−２ ）を 左右反転 してアウトプットるのですす。
次に、 図−Ｂ を見てください。 潜望鏡は鉛直に置かれています。 Ａ の位置から見ると、 図−４ になります。 鉛直に置かれた潜望鏡は、 インプットされた図（ Ｄの位置から見た上の字 ＝ 図−２ ）を 上下反転 してアウトプットするのです。
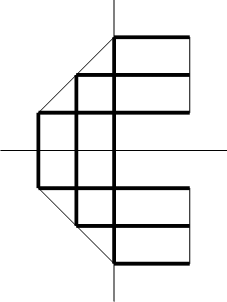
後側観察用潜望鏡に映る背景は 180°回転しています。
それは、まず、観察者が背景を相対的に 左右反転 し、
その後、後側観察用潜望鏡の合わせ鏡が背景を 上下反転 させているからです。
左右反転 と 上下反転 の合成は 180°回転です。
それは、まず、観察者が背景を相対的に 左右反転 し、
その後、後側観察用潜望鏡の合わせ鏡が背景を 上下反転 させているからです。
左右反転 と 上下反転 の合成は 180°回転です。
このことを理解するための簡単なアニメーションを十進BASIC で作ってみました。順に見ていくと理解しやすと思います。