【 問 題 1 】
-
長さ 20 cm の線分がある。その線分上に無作為に点を1つとり、そこで2分割する。そして長いほうの線分を選び、その線分を一辺とする正方形を作ってその面積を求める。これを無数回繰り返して平均をとると、その値はいくらになるか。
-
選んだ線分を一辺とする正方形の面積の期待値を求める。それは次の方法によって求められる。
1回の試行で選ぶ線分の長さを y とすると、 x ≦ y ≦ x + dx となる確率は次の式になる。
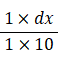
したがって、選んだ線分を一辺とする正方形の面積の期待値は次の式になる。
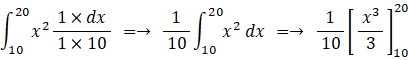
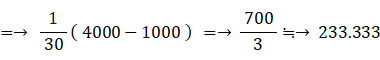
-
面積が 100 cm2 ~ 400 cm2 の正方形の中から無作為に1つの正方形を選んだとき、面積の期待値を求めよ。
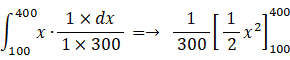
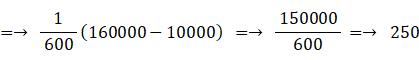
参考: ばいおりんの日常的物理学文集 > 錯覚と物理学 > 食い違う長さと面積の平均値
【 問 題 3 】
-
一辺の長さが 10 cm ~ 20 cm の正方形の中から無作為に1つの正方形を選んだとき、面積と一辺の長さの期待値を求めよ。
-
まずはプログラミングシミュレーションをしてみましょう。
シミュレーションの結果、次のようなことが分かります。
・ ① の値はおよそ 15 である。
・ ⑤ の値はおよそ 250 である。
・ ① < ④ ← どうして ① = ④ じゃないの? ( 疑問その1 )
・ ② < ⑤ ← どうして ② = ⑤ じゃないの? ( 疑問その2 )
・ ② > ③ ← どうして ② = ③ じゃないの? ( 疑問その3 )
・ ④ < ⑥ ← どうして ④ = ⑥ じゃないの? ( 疑問その4 )
プログラムの内容 :
① の求め方:
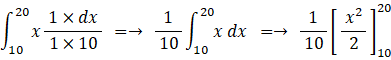
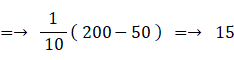
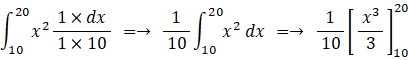
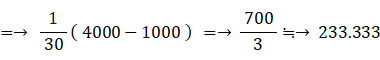
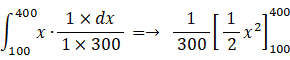
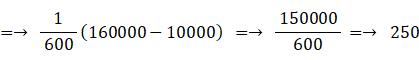
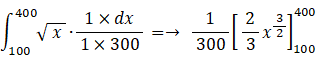
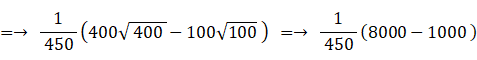
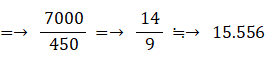
では、どうして ④ < ⑥ なのでしょうか? この点が本当のパラドックスです。疑問その4について考えていきましょう。
まず、2つの正方形で考えましょう。まず、一辺の長さが 1 m と 3 m の正方形で。 一辺の長さの平均は 2 m です。面積の平均は 5 m2 です。面積の平均の正の平方根は約 2.24 です。 2 < 2.24 です。次に、一辺の長さが 3 m と 5 m の正方形で。 一辺の長さの平均は 4 m です。面積の平均は 17 m2 です。面積の平均の正の平方根は約 4.12 です。 4 < 4.12 です。このように、2つの正方形の場合、面積の平均の正の平方根の方が一辺の長さの平均よりも必ず大きくなっています。それは、次の命題が真であることを証明することによって理解することができます。
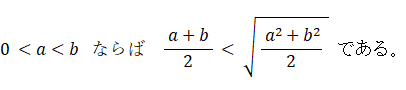
( 証 明 )
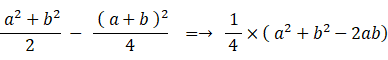
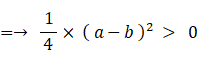
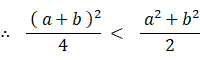
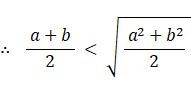
このようにしてみると、④ < ⑥ は当たり前のように思えてきます。いくら標本数を増やしても ④ < ⑥ は変わらないのです。したがって、 ④ = ⑥ でなくて当たり前ということになります。
※ 参照:
大学生のための数学 > 数理論 > 連続する自然数の和の平均 と 連続する自然数の2乗の和の平均の正の平方根
大学生のための数学 > JavaScript > JavaScript_シミュレーション > 地球儀の1点を選んだときの緯度の確率
 確率 へ戻る
確率 へ戻る