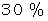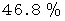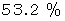数学と物理学 へ戻る私のバイオリンは気まぐれで、 良く響く日もあれば、 あまり響かない日もあります。 そこで、 １か月ごとに、 よく響いた日 と あまり響かなかった日 とに２分して、 いろんな要因との相関関係を調べてみました。 でも相関関係があったのはアルコール量だけでした。 しかし、 これは、 原因と結果が逆で、 よく響いた日には、 心がはずんで晩酌の量が増えたためだったのです。 しかし、 １つだけ手がかりがありました。 それは前日の結果との関係です。 およそ次のような法則があったのです。 よく響いた次の日は
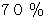の確率でよく響き、 あまり響かなかった翌日は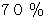の確率であまり響かないのです。今日、 バイオリンが良く響いたとします。 では、 毎日バイオリンを弾いて、 ３日後の老人ホーム慰問コンサートの時によく響く確率はいくらになるでしょうか。 また、 今日響かなかったとすれば、 ３日後の老人ホーム慰問コンサートの時によく響く確率はいくらになるでしょうか。
|
|
明日、 よく響く |
明日、 あまり響かない |
|
今日、 よく響いた |
|
|
|
今日、 あまり響かなかった |
|
|
遷移行列
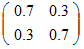
３日後の確率 ：
|
|
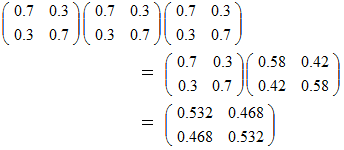
３日後、 よく響く |
３日後、 あまり響かない |
|
今日、 よく響いた |
|
|
|
今日、 あまり響かなかった |
|
|
したがって、 答えは、
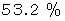と 
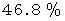です。ちなみに、 １年後の今日、 バイオリンがよく響く確率は、 今日の響き方に関わらず、 限りなく
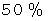に近くなります。 このことを、 「 この遷移行列の要素である 『 バイオリンがよく響く確率 』 は 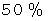に収束する。」 と言います。参考： 大学生のための数学 ＞ 線形代数学 ＞ マルコフ過程 と 遷移行列
お断り ：
この文章はフィクションであり、 事実とはかなり異なります。 その一例を申しますと、 私は、 はずかしがりやなので素面（しらふ）でバイオリンを弾くことはほとんどありませんし、 また、 他人様に聞いていただくようなものではありません。
JavaScript のプログラムによるシミュレーション：
プログラムの内容：