(1) 一般の曲線と物理学
円 : 回転している剛体の微小内部部分の軌道です。 球体のみかけの形です。
楕円 : 惑星の軌道です。
彗星の軌道は、 近日点のところで、
脱出速度より遅ければ、 楕円 になり、
脱出速度ちょうどであれば、 放物線 になり、
脱出速度より速ければ、 双曲線 になります。
放物線 : 一様な重力場において、 物を斜め上に投げたときの軌道です。
放物曲面は電磁波を焦点に集めるための反射鏡に使用されます。
双曲線 : 同時発射電磁波の受信時間差による位置確認システムで描かれます。
サインカーブ : 単振動を表します。
-
滑らずに転がる円の円周上のある点が描く軌跡です。
一様な重力場において球が最短時間で転がり落ちる曲線です。
また、 曲線上のどの位置から球を転がしても、 最下点まで行く時間が同じになる特徴があります。 最も単純なサイクロイドは、 媒介変数
 を用いて、 次のように表されます。
を用いて、 次のように表されます。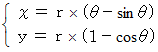
-
自転する円の円周上のある点の接線上を次第に円から遠ざかっていく描点の軌跡です。曲線上の点の法線( 接線に垂直 )はすべて一つの円に接します。
現代の歯車の歯形の大部分を占める曲線です。 製造が容易だからです。
-
非自転的回転をしている円の中心を中心として回転する描点の軌跡です。 特殊な場合、 サイクロイド曲線になったり、 楕円になったりします。
トロコイド曲線を歯車の歯形に使用した歯車は、 歯車ポンプ( 回転する歯車の接合部を使って液体を一方方向に輸送するポンプ )でよく使われています。
-
等速移動している車で、 ハンドルを等速円運動させたときの車の軌道です。 曲線上の点の始点からの道のりに曲率半径をかけたものは一定になっています。
道路のカーブはクロソイド曲線で作られます。
 数学と物理学 へ戻る
数学と物理学 へ戻る