(1) 2次元平面の曲線( その長さ と 接線 と 法線ベクトル )
-
XY平面上に曲線があるとします。 曲線が直線に近い時は、 曲線の長さは直線の長さで近似されます。 曲線を区間に分けて、 その区間の長さの総和で曲線の長さ表すことにします。 区間が微小であれば微小であるほどその区間の曲線は限りなく直線に近づいていきます。 したがって、 曲線の長さは次のようになります。
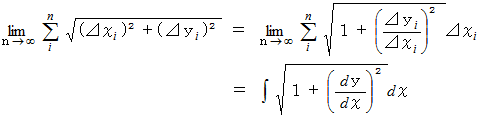
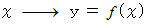 の写像が成り立っていて、 曲線が
の写像が成り立っていて、 曲線が 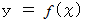 で表されるときは、 曲線の長さは次のように表されます。
で表されるときは、 曲線の長さは次のように表されます。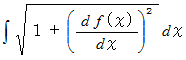
この式は、 曲線上の点の位置ベクトルから導く曲線の長さの公式からでも導くことができます。

曲線 :
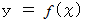 の単位接ベクトルは、次のように表されます。
の単位接ベクトルは、次のように表されます。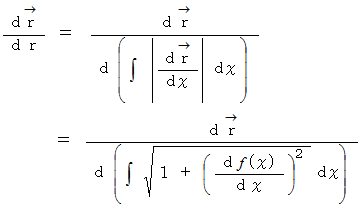
また、 曲線 :
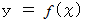 の単位接ベクトルは次のようにも表されます。
の単位接ベクトルは次のようにも表されます。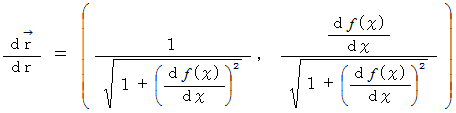
曲線 :
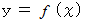 の 点
の 点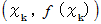 における接線は次のように表されます。
における接線は次のように表されます。
 なぜなら、 傾きが
なぜなら、 傾きが  で 点
で 点 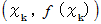 を通る直線だからです。
を通る直線だからです。曲線 :
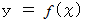 の単位法ベクトルは、 次のように表されます。
の単位法ベクトルは、 次のように表されます。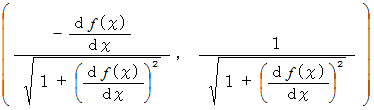
パラメーター表示 ( 物理学的表示法 ) :
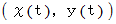 のときは、
のときは、曲線の長さの公式は次のようになっています。
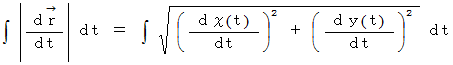
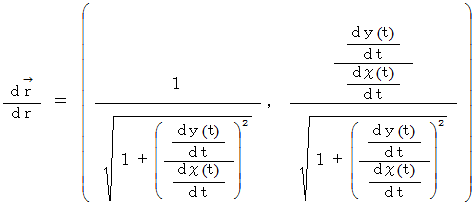
単位接ベクトルは次のように表されます。
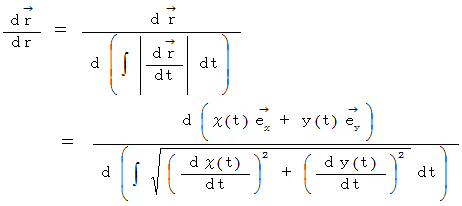
また、 単位接ベクトルは次のようにも表されます。
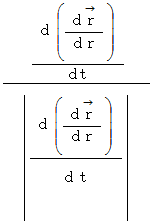
単位法ベクトルは次のように表されます。
また、 単位法ベクトルは次のようにも表されます。
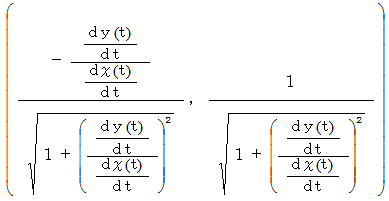
-
曲線の長さは次のようになります。
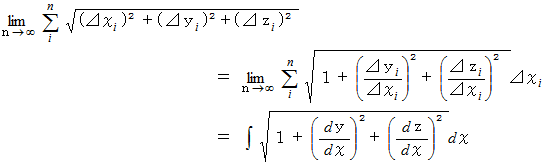
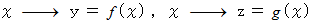 の写像が成り立っていて、 曲線上の点が
の写像が成り立っていて、 曲線上の点が 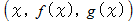 で表されるときは、 曲線の長さは次のように表されます。
で表されるときは、 曲線の長さは次のように表されます。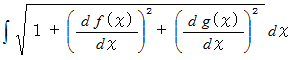
この式は、 曲線上の点の位置ベクトルから導く曲線の長さの公式からでも導くことができます。
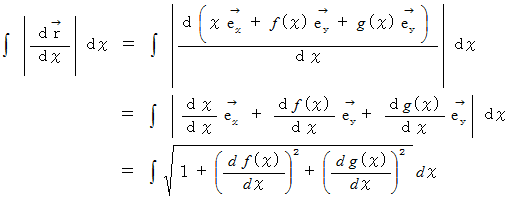
曲線 :
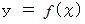 の単位接ベクトルは、 次のように表されます。
の単位接ベクトルは、 次のように表されます。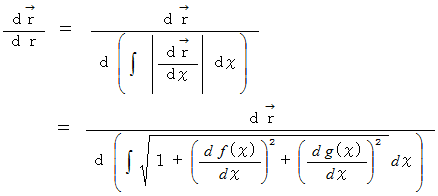
また、 曲線 :
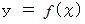 の単位接ベクトルは次のようにも表されます。
の単位接ベクトルは次のようにも表されます。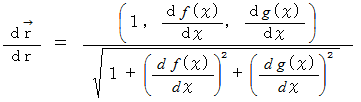
パラメーター表示 ( 物理学的表示法 ) のとき ;
点
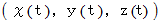 の位置ベクトルは次のように表されます。
の位置ベクトルは次のように表されます。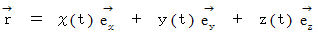
曲線の長さは次のように表されます。
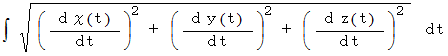
単位接ベクトルは次のように表されます。
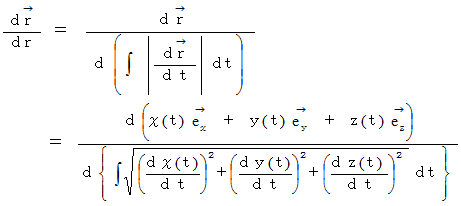
単位法ベクトルは次のように表されます。

例題 :
 の
の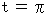 における 単位接ベクトル と単位法ベクトル を求めよ。
における 単位接ベクトル と単位法ベクトル を求めよ。( 答 え )
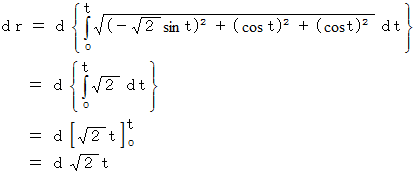
したがって、
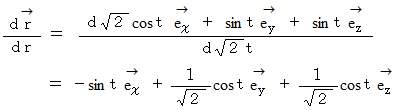
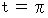 のとき、
のとき、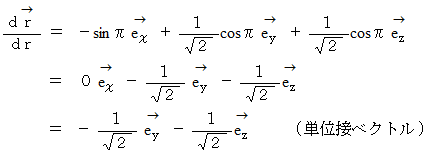
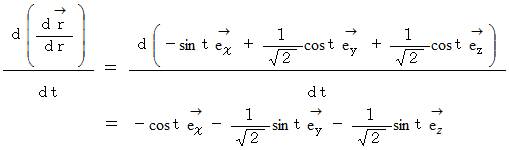
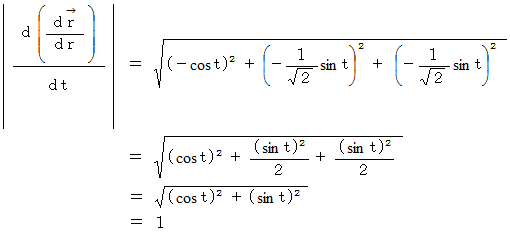
したがって、
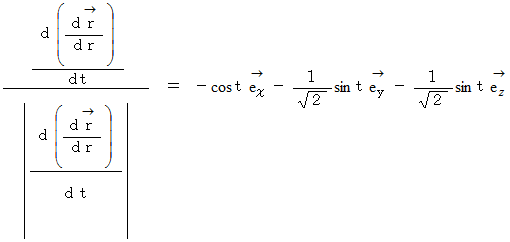
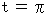 のとき、 上の式は次のようになる。
のとき、 上の式は次のようになる。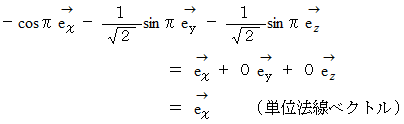
 ベクトル解析 へ戻る
ベクトル解析 へ戻る