３次元スカラー空間　f ( x, y, z ) を 長さ S の曲線 C ( x(t), y(t), z(t) ) に沿って線積分する式は、次のように表されます。
　　　
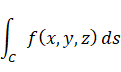
この式は次のようにも表すことができます。
　　　


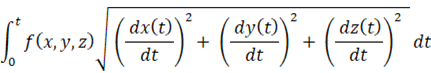
３次元ベクトル空間　f(→) ( x, y, z ) を 長さ S の曲線 C ( x(t), y(t), z(t) ) に沿って線積分する式は、次のように表されます。
　　　
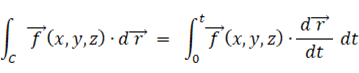
　しかし、ベクトル場の線積分の本質は、その点におけるベクトルと単位接線ベクトルの内積を積分するということで、本来は次の式で与えられます。
　　　
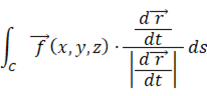
この式と上の式が同じものであることを今から説明します。
　　　
　　　　　　
　　　　　　
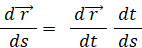
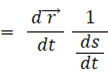
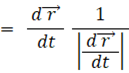
　　　よって、
　　　　　　
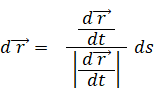
というわけで、この式と上の式が同じものであることが分かりました。
また、次のようにしても、この式と上の式が同じものであることがわかります。
　　　
　　　　　　　　　　　　　

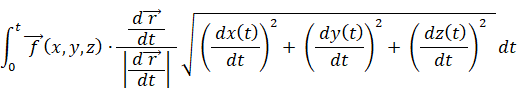
　ベクトル場の線積分の応用例は、物理学の「仕事」を求める式です。上記の式を見ると、仕事は力と速度の内積を時間で積分したものであることが分かります。ということは、等速円運動中に物質に作用する力は、物質に対して一切仕事をしていないというこです。力の方向と速度の方向が垂直だからです。

　※ 参照： 大学生のための数学 ＞ 解析学 ＞ スカラー場の線積分のイメージ