(1) 2次元平面の曲線の接線
 の値からなる集合と
の値からなる集合と  の値からなる集合があり、 前者から後者への写像を次のように表します。
の値からなる集合があり、 前者から後者への写像を次のように表します。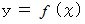
 は全ての実数として、
は全ての実数として、  ,
,  の直交2次元座標を用いて、 上記の写像 ( 関数 ) を表すと、 曲線になります。
の直交2次元座標を用いて、 上記の写像 ( 関数 ) を表すと、 曲線になります。曲線 :
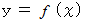 の 点
の 点 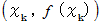 における接線は次のように表されます。なぜなら、傾きが
における接線は次のように表されます。なぜなら、傾きが 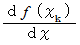 で 点
で 点 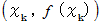 を通る直線だからです。
を通る直線だからです。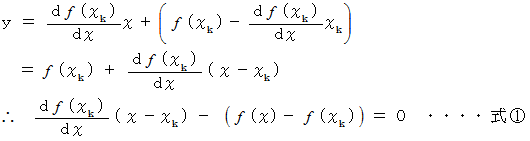
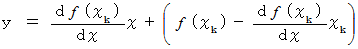 に直交し原点を通る直線は、 次のように表されます。
に直交し原点を通る直線は、 次のように表されます。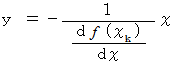
この直線は
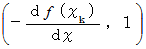 や
や 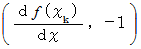 を通ります。
を通ります。とうことは、
 は、 ベクトル
は、 ベクトル 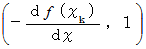 や ベクトル
や ベクトル 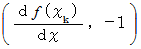 に直交します。
に直交します。ということは、 これらのベクトルは曲線の点
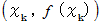 における法線の方向を表しているということで、 法線ベクトルと呼びます。
における法線の方向を表しているということで、 法線ベクトルと呼びます。 の値 と
の値 と  の値とのペアからなる集合 と
の値とのペアからなる集合 と 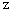 の値からなる集合があり、 前者から後者への写像を次のように表します。
の値からなる集合があり、 前者から後者への写像を次のように表します。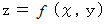
 と
と  は全ての実数として、
は全ての実数として、  ,
,  ,
, 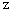 の直交3次元座標を用いて、 上記の写像 ( 関数 ) を表すと、 曲面になります。 この曲面の 点
の直交3次元座標を用いて、 上記の写像 ( 関数 ) を表すと、 曲面になります。 この曲面の 点 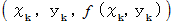 における接平面を求めてみましょう。
における接平面を求めてみましょう。 参 照
参 照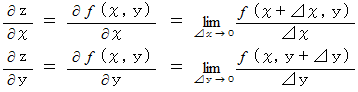
曲線の接線の式を応用すると曲面の接平面の式になります。
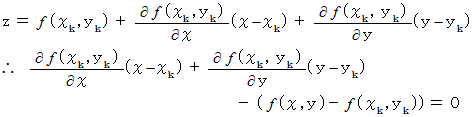
この平面は、 ベクトル
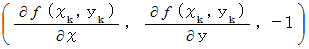 に直交します。
に直交します。このベクトルに逆向きのベクトルは
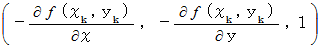 です。
です。ということは、
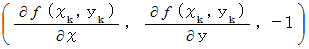 や
や 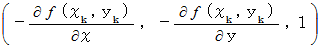 は、 曲面の点
は、 曲面の点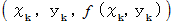 における法線ベクトルであるということです。
における法線ベクトルであるということです。この曲面は、 次の式で表されます。
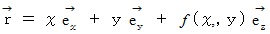
これは、 この曲面上の点の位置ベクトルを表したものです。
この曲面の単位法ベクトルは、 次の式で与えられます。
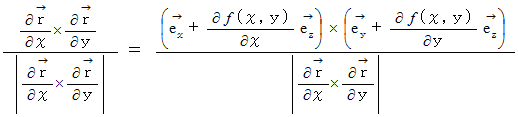
これを計算すると、 次のようになります。
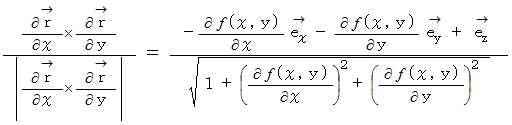
 ベクトル解析 へ戻る
ベクトル解析 へ戻る