以前に、純正調では、♯が付くと音の振動数は 25/24 倍になり、♭が付くと音の振動数は 24/25 倍になると書きましたが、今思うとそれは特定の条件の元でのことでした。特定の条件とは、古関裕而 作曲の「長崎の鐘」のように長調と短調の間での転調がある場合です。
しかし、長調と長調の間での転調( 移調 )の場合は違うのです。例えば、ト長調からニ長調への転調の場合は、ファ に♯が付くと音の振動数は 135/128 倍になります。
純正調における、ファ に対する ソ の振動数比:

純正調における、シ に対する ド の振動数比:
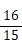
ト長調の ♯ファ ソ =→ ニ長調の シ ド
ト長調の ソ と ニ長調の ド は同じ振動数の音です。
ト長調の ファ の音の振動数を x とし、ニ長調の シ の音の振動数を k x とすると、
x × 9/8 = k x × 16/15
よって、 k = 9/8 ÷ 16/15 =→ 135/128
非移調時の #ファ : 移調時の #ファ = 25/18 : 4/3 × 135/128
=→ 25/18 : 45/32 =→ 1.0000:1.0125
※ 参考: 音楽と物理学 > オイラーによる純正調の数学的解析
平均律では、
#は、振動数を
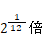 しなさいという意味になります。
しなさいという意味になります。♭は、振動数を
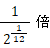 しなさいという意味になります。
しなさいという意味になります。純正調では、
-
長調と短調の転調においては、
#は、振動数を
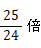 しなさいという意味になります。
しなさいという意味になります。♭は、振動数を
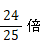 しなさいという意味になります。
しなさいという意味になります。長調どうしや短調どうしの転調においては、
#は、振動数を
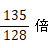 しなさいという意味になります。
しなさいという意味になります。♭は、振動数を
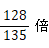 しなさいという意味になります。
しなさいという意味になります。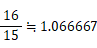


 音楽と物理学 へ戻る
音楽と物理学 へ戻る