n 手目直後の状態が A または B または C または D になる確率は 1 で、 そのすべての場合の数は 3n です。 これから、 n 手目直後の状態がAになる確率 P(n) を調べてみましょう。
まず、 次のことは簡単に解ります。
P(1) = 0 P(2) = 1 / 3
(n−1) 手目直後の状態がAの場合は n 手目直後の状態がAになることはなく、 (n−1) 手目直後の状態がA以外の場合は、n 手目直後の状態がAになる確率は 1 / 3 です。 (n−1) 手目直後の状態がA以外になる確率は 1 − P(n−1) ですので、 P(n)は次のようになります。
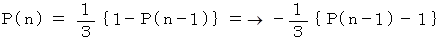
この漸化式を解くには、 特性方程式を作ります。
つまり、P(n) = x 、 P(n−1) = x と置いた式を作ります。
3x = 1 − x よって、 x = 1 / 4
したがって、 この漸化式は次のように変形することができます。
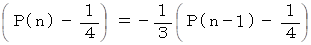

したがって、
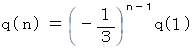
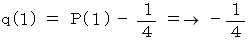
したがって、
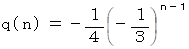
よって、
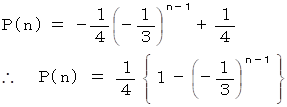
具体的には次のようになります。
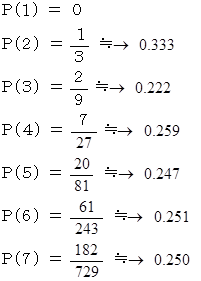
シミュレーション :
プログラムの内容 :
n 手目直後の状態がAになる確率が分かれば、 n 手目直後の状態がAになる移動のすべての場合の数 F(n) が分かります。 それは次の式から求めることができます。
F(n) = 3n × P(n)
具体的には次のようになります。
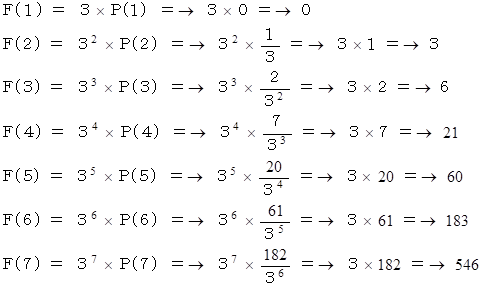
 確率 へ戻る
確率 へ戻る