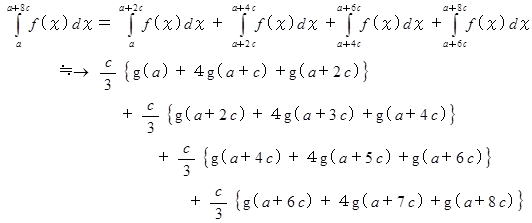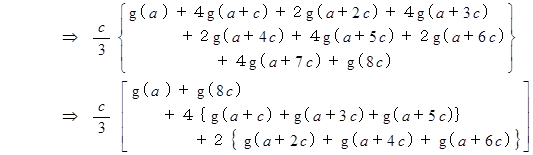ある曲線
 の微小区間
の微小区間 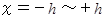 における定積分について考えましょう。
における定積分について考えましょう。 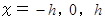 における曲線上の3点を通る放物線を定積分することで、 その曲線の微小定積分を近似することにします。
における曲線上の3点を通る放物線を定積分することで、 その曲線の微小定積分を近似することにします。その放物線を
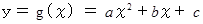 とします。
とします。
ここで、 次の式が成り立ちます。

したがって、
 は次のようになります。
は次のようになります。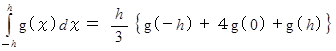
したがって、 次の式が成り立ちます。
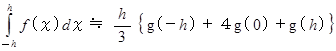
上の式は、 一般的に次のように表されます。
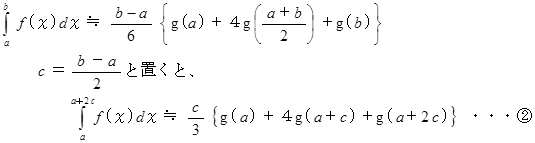
 より
より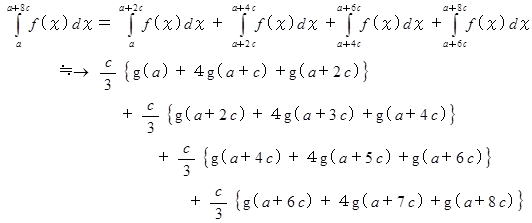
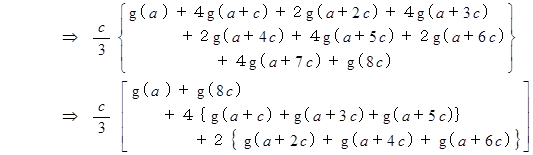
この式は、 シンプソン公式を表しています。
次の十進BASIC のプログラムは、 シンプソン公式を用いて定積分の近似値を求めるものです。
 解析学 へ戻る
解析学 へ戻る 大学生のための数学 へ戻る
大学生のための数学 へ戻る の微小区間
の微小区間 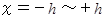 における定積分について考えましょう。
における定積分について考えましょう。 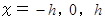 における曲線上の3点を通る放物線を定積分することで、 その曲線の微小定積分を近似することにします。
における曲線上の3点を通る放物線を定積分することで、 その曲線の微小定積分を近似することにします。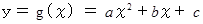 とします。
とします。

 は次のようになります。
は次のようになります。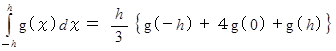
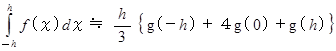
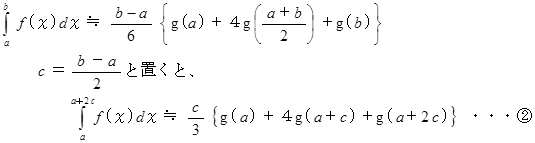
 より
より