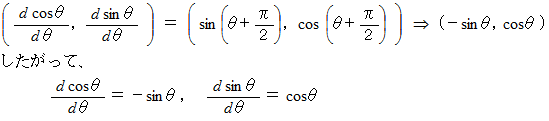(1) スタンダードな三角関数の微分の証明法
-
加法定理 :
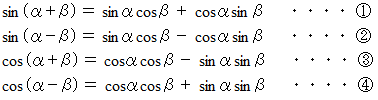
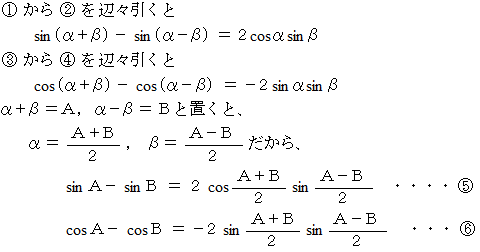
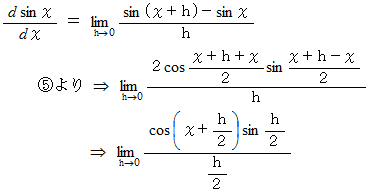
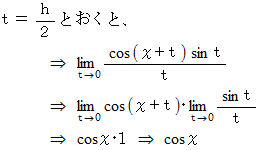
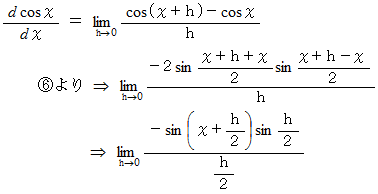
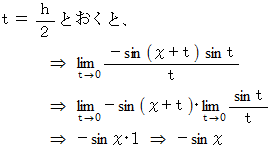

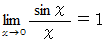 の理由については、次の論文を見てください。
の理由については、次の論文を見てください。解析学 > 三角関数の極限値の公式
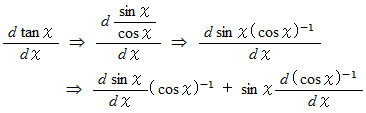
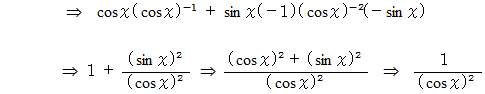
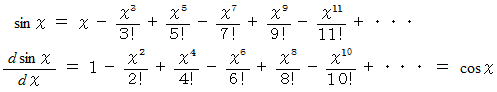
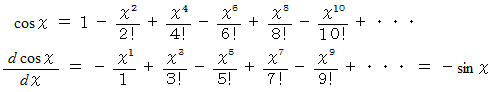
(3) 周期
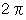 で 半径
で 半径  の円周上を反時計回りに等速回転している点を用いる方法
の円周上を反時計回りに等速回転している点を用いる方法-
点の速度
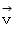 の大きさは、
の大きさは、  に
に 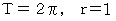 を代入して、 次のようになります。
を代入して、 次のようになります。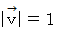
点の位置ベクトルを
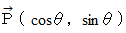 で表すと、 点の速度は次のようになります。
で表すと、 点の速度は次のようになります。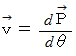
したがって、
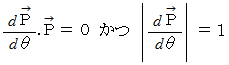
上記の条件を満たす
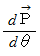 の成分は
の成分は 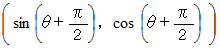 です。
です。一方、
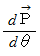 の成分は
の成分は 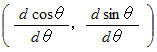 です。
です。したがって、
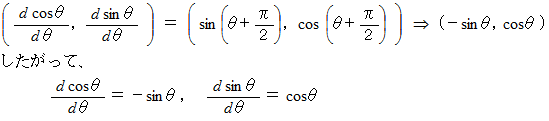
 解析学 へ戻る
解析学 へ戻る 大学生のための数学 へ戻る
大学生のための数学 へ戻る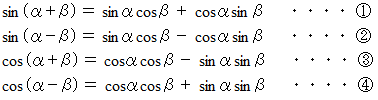
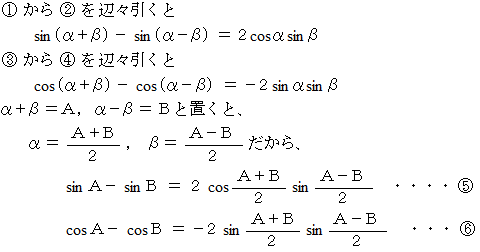
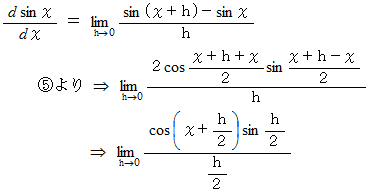
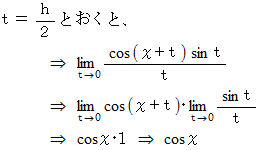
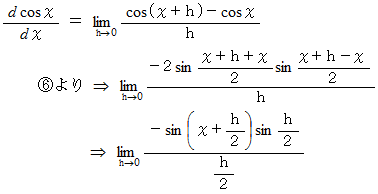
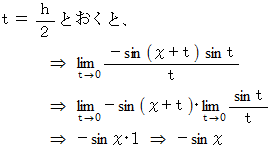

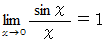 の理由については、次の論文を見てください。
の理由については、次の論文を見てください。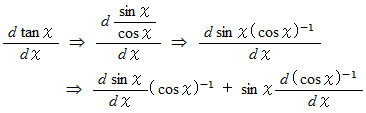
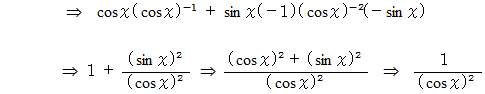
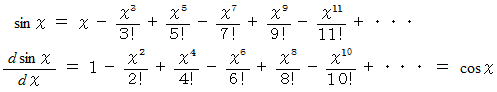
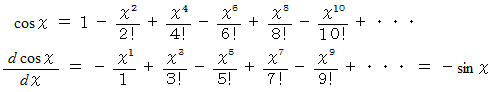
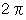 で 半径
で 半径  の円周上を反時計回りに等速回転している点を用いる方法
の円周上を反時計回りに等速回転している点を用いる方法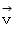 の大きさは、
の大きさは、  に
に 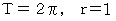 を代入して、 次のようになります。
を代入して、 次のようになります。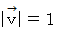
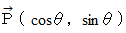 で表すと、 点の速度は次のようになります。
で表すと、 点の速度は次のようになります。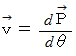
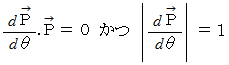
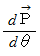 の成分は
の成分は 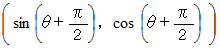 です。
です。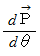 の成分は
の成分は 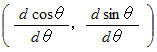 です。
です。