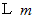 離れた平行線上を質量
離れた平行線上を質量 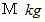 と
と 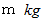 の2つの質点が逆方向に相対的な速さ
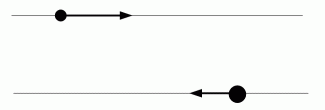
の2つの質点が逆方向に相対的な速さ 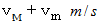 で等速直線運動をしています。 非現実的な設定で恐縮ですが、 2つの質点が最短距離になるまでは互いの重力は作用せず、 最短距離になった瞬間から後ずっと重力が作用するものとします。 次の条件を満たす時、
で等速直線運動をしています。 非現実的な設定で恐縮ですが、 2つの質点が最短距離になるまでは互いの重力は作用せず、 最短距離になった瞬間から後ずっと重力が作用するものとします。 次の条件を満たす時、 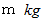 の質点は重力によって 速さ
の質点は重力によって 速さ 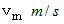 で等速円運動を開始します。
で等速円運動を開始します。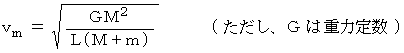
このときの公転中心の位置を求めてみましょう。 公転中心は、 2つの質点が最短距離になったときの2つの質点を結ぶ線分上にありそうです。 したがって、 その線分上の
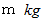 の質点から
の質点から 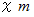 離れた点を公転中心であるとし、
離れた点を公転中心であるとし、  を求めることにします。 2つの質点が最短距離になったときの
を求めることにします。 2つの質点が最短距離になったときの 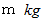 の質点が受ける重力は次の式で表されます。
の質点が受ける重力は次の式で表されます。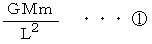
速さ
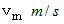 で等速円運動をする
で等速円運動をする 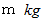 の質点に作用する遠心力は次の式で表されます。
の質点に作用する遠心力は次の式で表されます。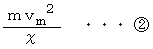
 と
と  は相殺しますので、 次の式が成り立ちます。
は相殺しますので、 次の式が成り立ちます。
これが求めるものですが、 この式より次の式が成り立ちます。
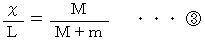
これは、 2つの質点の系の重心の位置を表すものです。 2つの質点の系の重力による質点の公転中心は、 2つの質点の系の重心になっているのです。 このとき重心の
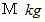 の質点からの距離を
の質点からの距離を 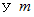 とすると、 次の式が成り立ちます。
とすると、 次の式が成り立ちます。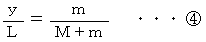
 は 次のように
は 次のように  から導かれます。
から導かれます。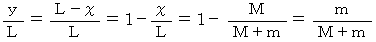
さて、
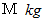 の質点は速さ
の質点は速さ 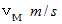 で重心の周りを等速円運動し始めます。
で重心の周りを等速円運動し始めます。 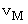 は次の式で表されることを証明してみましょう。
は次の式で表されることを証明してみましょう。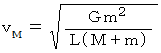
2つの質点が最短距離になったときの
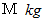 の質点が受ける重力は
の質点が受ける重力は  の式で表されます。 また、 遠心力は次のようになります。
の式で表されます。 また、 遠心力は次のようになります。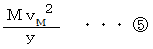
 と
と  は相殺しますので、 次の式が成り立ちます。
は相殺しますので、 次の式が成り立ちます。
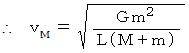
 力学 へ戻る
力学 へ戻る