（ 問 題 ）

次の式が成り立つことを証明しなさい。
　　　

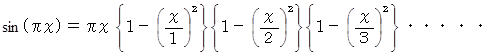
　　　　　　　ただし、 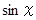のマクローリン展開は次の式で表されます。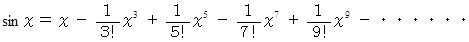
　　　　　　　　　　　

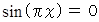（ 証 明 ）

　の解は、 次のように表されます。

　　　　　　　　＝　・ ・ ・ ・　−３， −２， −１， ０， １， ２， ３，　・ ・ ・ ・

したがって、
　　　　

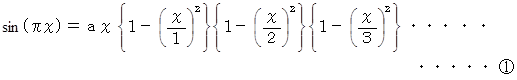
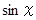のマクローリン展開式より、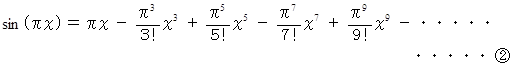
　　　　

と の　 の項を比較すると、 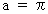ですので、 次のようになります。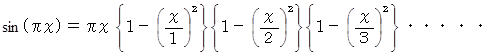
　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（ 証明終わり ）

と　 の 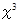の項を比較すると、 次のようになります。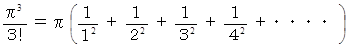
　　　　
　　　　
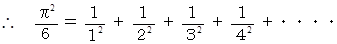
これは、 オイラーによって発見された 平方数の逆数の和の収束値 です。