現実の世界では「 永久機関 」を作ることは不可能ですが、 アートの世界では「 無限階段 」を作ることが可能です。 私は構成失行があるためにそれをここに描くことができませんが、「 ペンローズ　無限階段 」でインターネット検索するとヒットしますので、 ご覧ください。 ということで、 今日は「 錯視 」の例を２つほど紹介したいと思います。

　 次の図の三角形の中の点は、 三角形の重心です。 それぞれの頂点から向かい合う辺に下した垂線の交点です。

　　　　　

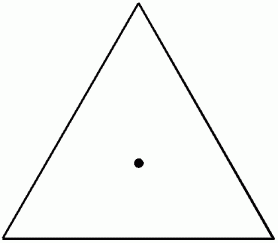
では、 次の図の三角形の中の点は、 どんな点でしょう？　（ 問題１ ）

　　　　　



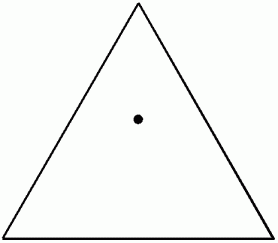
次の図のように、 まず、 図形を分割します。

　　　　　

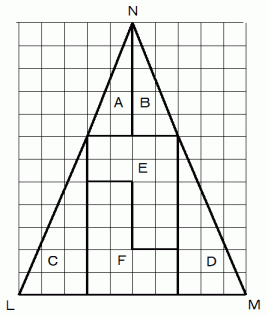
　 そして、 次のように並び替えると、 灰色の部分の穴ができます。 底辺と高さが等しい三角形は面積が等しいはずなのに、 何故でしょうか？　（ 問題２ ）

　　　　　


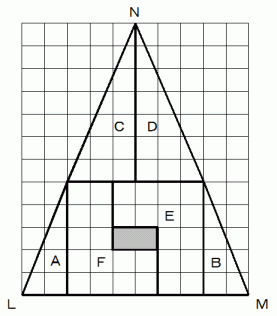
　問題１ の答え ：
　　　 　頂点から底辺に下した垂線の中点、 つまり、 高さの半分の点です。

　問題２ の答え ：
　 　　　三角形だと思っていた図形 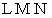は、三角形ではなく五角形だったのです。 最初
　　　は凹の五角形で、 後は凸の五角形です。 凹の五角形とは、 １つ以上の内角が180度
　　　よりも大きい五角形のことです。 これはアメリカの数学者カリーが考案したものです。