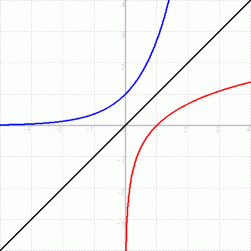
指数関数　y ＝ ａ^x　のグラフ （ 青色 ） と 対数関数　y ＝ log_ａx のグラフ （ 赤色 ） は 直線　y ＝ x に関して対称です。 つまり、 直線　y ＝ x に関する 対数関数　y ＝ log_ａx のグラフ の鏡像は、 指数関数　y ＝ ａ^x　のグラフと同一です。なぜなら、 指数関数　y ＝ ａ^x　と　対数関数　y ＝ log_ａx　が逆関数の関係になっているからです。


【 問 題 】

点 ( x, y ) の直線 y ＝ x に対する鏡像は 点 ( y, x ) であることを証明せよ。

　【 解 答 】

　点Ｐ ( P_x , P_y ) を通り直線 y ＝ x に垂直な直線の方程式は　y−P_y ＝ −(x−P_x )　である。
　点Ｐ ( P_x , P_y ) の直線 y ＝ x に対する鏡像を 点Ｑ ( x, y ) とする。
　線分ＰＱの中点を点Ｍとすると、点Ｍ ( ( x＋P_x) / 2 ,　( y＋P_y) / 2 ) となる。
　点Ｍは、２つの直線　y ＝ x　と　y−P_y ＝−( x−P_x )　の上に存在するので、次の２つの式が成り立つ。
　　　y＋P_y ＝ x＋P_x
　　　y−P_y ＝−x＋P_x
　上記の２つの式を連立して解くと、
　　　y ＝ P_x　　x ＝ P_y
　よって、点Ｐ ( P_x , P_y ) の直線 y ＝ x に対する鏡像は 点Ｑ ( P_y , P_x) である。
　というわけで、点 ( x, y ) の直線 y ＝ x に対する鏡像は 点 ( y, x ) であることが明らかになった。

　【 別 解 】

　原点を中心に反時計回りに π ラジアン回転する写像は、座標系を時計回りに π ラジアン回転する座標変換と表現上は同じことであるように、直線 y ＝ x に対する鏡像へと変換する写像は、座標系を直線 y ＝ x に対する鏡像へと変換する座標変換と表現上は同じことである。したがって、次のような手はずを取ることになる。


直線　y ＝ x に関して鏡像となる座標系への座標変換
　　　
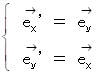
基底変換テンソル ：
　　　
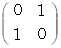
座標変換テンソル ：
　　　
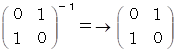
したがって、 座標変換式は、
　　　

（ 追 伸 ）

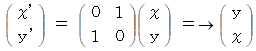
　対数関数　y ＝ log_ａx の 直線 y ＝ x に対するの鏡像のグラフが 指数関数　y ＝ ａ^x　のグラフと同じになるのは、次のように変換されるからです。
　　　y ＝ log_ａx　　→　　x ＝ log_ａy　　→　　y ＝ ａ^x