（１）　Ｎ は ２ の何乗？

　　　　　　　　

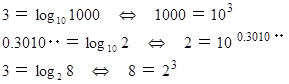
先生 ：
　 「 Ｎ は 10 の何乗ですか？」 と尋ねられたら、 「 Ｎ は 10 の 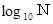乗です。」 と答えればいいのです。 たとえば Ｎ が 500 のときは、 関数電卓を用いて 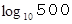を求め、 500 は 10 の 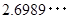乗であることがわかります。 では、 「 Ｎ は ２ の何乗ですか？」 と尋ねられたらどう答えますか？

生徒Ａ ：
　 「 Ｎ は ２ の 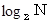乗です。」 と答えます。

先生 ：
　 そうですね。 しかし、 これでは関数電卓を使って具体的な値を求めることができません。
　 それ以外の答え方はないでしょうか？

生徒Ａ ：
　 ・ ・ ・ ・ ・ ・ ・ ・ ・ ・

先生 ：
　 ヒントは　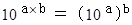　です。
　 そして、

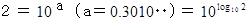
生徒Ａ ：
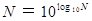　 　だから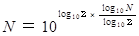　
　 よって、
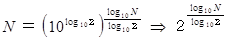
　 そうか、 ２ の 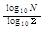乗 ですね。

先生 ：
　 正解です。 このことより、 次の式が成り立っていることがわかりますね。
　　　　　　
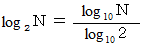
　 この式は 「 対数の底の変換公式 」 になっています。 この公式を知っていた人はすぐに答えがでたと思います。 今 Ａ さんが考えてくれたことは 「 対数の底の変換公式 」 の証明です。

　 では、 ある自然数が２の何乗になっているかを教えてくれる十進BASIC のプログラムを作ってみましょう。

　　　　INPUT
　　　　PROMPT　" ２の何乗？ 調べたい自然数は？ " : N
　　　　LET　P = LOG10 ( N ) / LOG10 ( 2 )
　　　　PRINT　N ; " は ２ の " ; P ; " 乗 です。"
　　　　END


　 したがって、 ある自然数 を ある自然数を底とする指数 で表現するためのプログラムは次のようになります。

　　　　INPUT PROMPT " 指数化したい ０よりも大きい有理数は？ " : N
　　　　INPUT PROMPT " 底は？　自然数でお願いします。　" : M
　　　　LET　 P = LOG10 ( N ) / LOG10 ( M )
　　　　PRINT　N ; " は " ; M ; " の " ; P ; " 乗です。"
　　　　END





（２）　１０進数を２進数に変換する十進BASIC のプログラム

１０進数を２進数に変換する十進BASIC のプログラムには次のようなものがあります。

　　　　OPTION BASE 0
　　　　INPUT PROMPT ; " ２進数に変換したい数は？ （ ２５５以下の自然数 ） " : n
　　　　LET　C = n
　　　　DIM　B ( 15 )
　　　　FOR　I = 0　TO　7
　　　　　　LET　B ( I ) = MOD ( C, 2 )
　　　　　　LET　C = INT ( C / 2 )
　　　　NEXT　I
　　　　FOR　I = 7　TO　0　STEP −1
　　　　　　PRINT　B ( I ) ;
　　　　NEXT　I
　　　　END
　　　　　　　　　　　　　　　　　　　　　　　MOD ( a, b ) ：　a を b で割った余り
　　　　　　　　　　　　　　　　　　　　　　　INT ( c ) ：　c を超えない最大の整数



しかし、 これよりも美しいプログラムが 2013年度のセンター試験で紹介されました。

　　　　INPUT PROMPT " ２進数に変換したい数は？ " : N
　　　　LET　P = INT ( LOG10 ( N ) / LOG10 ( 2 ) )
　　　　LET　X = 2 ^ P
　　　　FOR　I = 1　TO　P + 1
　　　　　　PRINT　INT ( N / X ) ;
　　　　　　LET　N = N − INT ( N / X ) * X
　　　　　　LET　X = X / 2
　　　　NEXT　I
　　　　END



　 ＜ コピペ用の小窓 ＞