確率 へ戻る-
ある患者は心室性期外収縮（ ＶＰＣ ）が 1 分間に平均６回出現する。 今、 この患者にＶＰＣが起こったが、 （１） 今後、 ＶＰＣが、 ５秒以内、 10秒以内、 15秒以内、 30秒以内 に １ 回以上起こる確率をそれぞれ求めよ。 また、（２） 今後、 最初のＶＰＣが、 ５秒以内、 ５秒〜10秒の間、 10秒〜15秒の間、 30秒以降 に起こる確率をそれぞれ求めよ。
-
（１）
この手の確率は、 指数分布
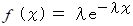の累積分布関数 
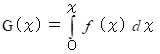に従う。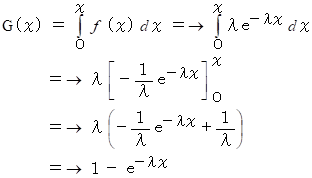
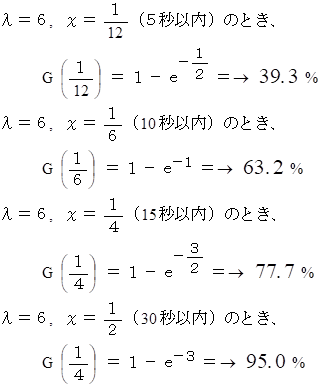
（２）
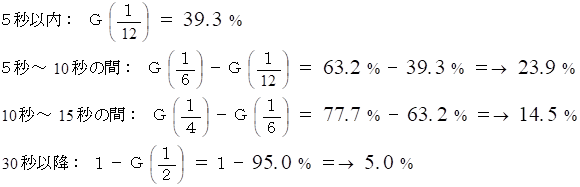
１ つのＶＰＣが出現してから ５ 〜 10秒後の間に起こるＶＰＣの回数の期待値 と 10 〜 15 秒後の間に起こるＶＰＣの回数の期待値 は どちらも １ 回で同じです。 しかし、 １つのＶＰＣが出現してから初めて出現するＶＰＣが出現するのは、 10 〜 15 秒後の間 よりも ５ 〜 10 秒後の間 のほうが圧倒的に多いのです。 というわけで、 次のＶＰＣが出現する確率は、 その前のＶＰＣが出現してから時間が経過していないほど高くなります。 こうした確率分布が指数分布というわけです。
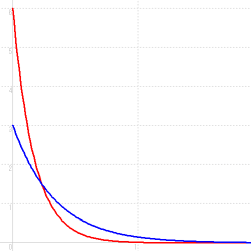
次の図の赤色は λ ＝ ６ の場合の指数分布であり、 青色は λ ＝ ３ の場合の指数分布です。
LET E = 2.71828
LET r1 = 6
LET r2 = 3
DEF f(x) = r1 * ( 1 / e^r1 ) ^ x
DEF g(x) = r2 * ( 1 / e^r2 ) ^ x
SET WINDOW -0.1, 1.9, -0.2, 6.2
DRAW grid
SET LINE width 3
SET LINE COLOR 4
FOR x = 0 TO 120 STEP 0.01
PLOT LINES: x, f(x);
NEXT x
PLOT LINES
SET LINE COLOR 2
FOR x = 0 TO 120 STEP 0.01
PLOT LINES: x, g(x);
NEXT x
END
平均で１分間に６回の割合で出現するということは、 平均で 1 / 6 分間 （ 10 秒間 ） に１回 の割合で出現するということです。 したがって、 次のＶＰＣが出現するまでの時間の平均は 10 秒間になることは分かります。 では、 その散らばり具合はどうでしょう？ 上の図を見るとイメージは出来ると思いますが、 シミュレーションプログラムを動かして確かめてみましょう。
プログラムの内容 ：
「 平均して１時間に６人の来客がある店がある。 ある客が入ってから次の客が入るまでに 31 分間あった。 これは特別なケースであると言い切ることができるか？ 有位水準 95 %（ 危険率 5 % ）で答えよ。」という統計学の問題も、 指数分布を使って解くことができます。 この店にとって 30 分間に客が １ 人も入らないという状況は 5.0 % の確率であり、 31 分間では 5 % 未満の確率になるので、 これは特別なケースであると言い切ることができます。