質量中心（ ２物質系の重心 ）には、その物質系の物質の質量の合計が集中しており、かつ、物質系の物質に作用しているすべての外力の合計が作用していると考えることができ、それらを用いて、質量中心の運動方程式を立てることができます。もし、保存力（ 物質に作用する力がする仕事が経路によらず一定になるような力 ）以外の外力の合計が 0 N の場合は、質量中心の加速度の大きさは 0 m/s² になり、この場合は、質量中心は静止を含む等速直線運動をします。

　２物質系において、保存力以外の外力の合計が 0 N をキープしたまま、物質間に働く内力によって物質の位置関係が変化すると、質量中心の存在する場所は移動しますが、質量中心は静止を含む等速直線運動をします。


【 問 題 】

　一様な密度をした質量 10 kg の底面が直角二等辺三角形（ 底辺の長さ＝120cm ）をした三角柱を図のように机の上に寝かして置きます。三角柱と机の間には摩擦は働かないものとします。
　一様な密度をした質量 10 kg の立方体（ 一辺の長さ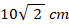＝ ）を図のように置いて静かに手を離し三角柱の斜面をさっと滑らせます。すると、三角柱は机の上を立方体が滑る方向の水平成分と反対方向に移動しますが、その距離を求めてください。なお、立方体と三角柱との間には摩擦は働かないものとします。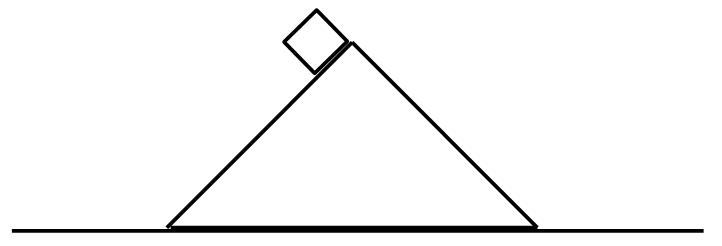

　　　

【 解 答 】

　立方体と三角柱を１つの物質系として見ると、この問題の運動に関しては保存力以外の外力が一切作用していません。つまり、保存力以外には作用反作用の関係にある内力しか作用していません。そして初期条件では質量中心は静止しています。したがって、質量中心 ( 重心 ) の存在する場所は移動するけれども（ G₀ → G₁ ）、質量中心の存在する位置は変化しません。よって、最初の質量中心の存在する場所 と 最後の質量中心の存在する場所 との距離が、三角柱が机の上を移動する距離になります。

　　　

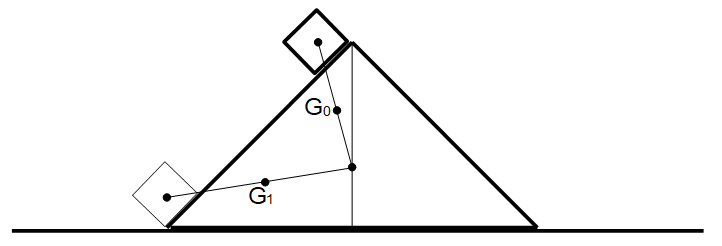
　G₀ は三角柱の質量中心軸のある場所より左側に 5 cm 偏位しており、G₁ は三角柱の質量中心軸のある場所より左側に 30 cm 偏位しています。
したがって答えは、25 cm です。