１回転するのに、 10秒かかるのと12秒かかるのとでは、 後者のほうがゆっくりと回転しています。１回転すると、 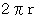の距離だけ転がりますが、 １回転するのに10秒かかるのと12秒かかるのとでは、 後者のほうがゆっくりと移動しています。

　「 万物の活動や移動がスローになる。」ことを、「 時計が遅れる。」とか「 時間が伸びる。」とかいう言葉で表現することがありますが、 それでは誤解されてしまいます。

　「 時計が遅れる。」という言い方をしますと、 たとえば、「 移動している時計の針の回転スピードは遅れている。」とは、「 普遍的なスピードで活動している万物の活動スピードは、 静止している時計で計測するのに比べて、 移動している慣性系の時計で計測すると、 速くなる。」である、 と誤解されることがあります。 ですから、「 時計が遅れる。」という言い方は、「 時間が遅れる。」という言い方に変えるべきです。 いや、「 時の経過スピードが遅くなる。」とか、「 万物の活動がスローになる。」というべきです。

　「 時間が伸びる。」という言い方をしますと、 たとえば、「 移動している慣性系の時間は２倍に伸びている。」とは、「 静止している慣性系の時が１時間経過する間に、 移動している慣性系の時が２時間経過している。」である、 と誤解されることがあります。 ですから、「 時間が伸びる。」という言い方は、「 時間が遅れる。」という言い方に変えるべきです。 いや、「 時の経過スピードが遅くなる。」とか、「 万物の活動がスローになる。」というべきです。


　 相対性理論は、 時間と空間を「 時空間の基底の要素 」と捉えています。 ならば、 時間と空間の単位は同じにすべきです。 簡単にするために、 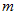（ は光の速さ ）を １秒 とする単位系を用い、 かつ、 横軸が空間で縦軸が時間の２次元直交時空間座標系とします。 ある時刻に原点に存在する４つの点状物質を、 限りなく薄いガラス板に描かれた直交座標の原点に重なる４つの点で表すことにします。

　 点状物質Ａは、 空間を移動せず、 一定のスピードで時間だけを正の方向に移動するものとします。 点状物質Ｂは、 時間を移動せず、 点状物質Ａと同じスピードで空間だけを正の方向に直線的に移動するものとします。 私たちの世界では、 点状物質Ｂは実在しません。 また、 点状物質Ｂは、 ドラえもんの「 どこでもドア 」のように瞬間移動しますが、 タイムトラベルはしません。 タイムトラベルに関して言いますと、 理論的には過去にはいけないのです。 また、 タイムトラベルが可能なものは、 普遍的な万物の時間の移動の速さと異なる速さで時間を移動できるのものなのですが、 そんなものは実在しないように思えます。 ただし、 瞬間冷凍解凍などの手段で老化しないで未来に行ける独りよがりな未来型タイムトラベルは可能です。 話が横道に逸れてしまいましたが、 点状物質Ｃは、 点状物質Ａと点状物質Ｂの時空間移動をベクトル的に合成したものであるとします。 すると、 点状物質Ｃは光子になります。 点状物質Ｄは、 速さ で空間を直線的に移動し、 かつ、 他の点状物質と同じスピードで時間を移動するものとします。

　 点状物質Ａの10秒間の時空間移動（ 点状物質Ａの場合は、 時間のみ移動である。）は、 その間に絶え間なく新たなガラス板に存在位置を記して、 順にガラス板を重ねていき、 それを真上から眺めた２次元平面における、 原点を一端とする時間軸上の長さ10秒間の線分で示されます。
　 点状物質Ｂの10秒間の時空間移動（ 点状物質Ｂの場合は、 空間のみ移動である。）は、 その間に絶え間なく新たなガラス板に存在位置を記して、 順にガラス板を重ねていき、 それを真上から眺めた２次元平面における、 原点を一端とする空間軸上の長さ10秒間の線分で示されます。
　 点状物質Ｃの10秒間以上の時空間移動（ 空間の単位も秒です ）は、 その間に絶え間なく新たなガラス板に存在位置を記して、 順にガラス板を重ねていき、 それを真上から眺めた２次元平面における、 原点を一端とする線分で示されます。 その線分上の点の時間軸からの距離と空間軸からの距離は等しくなっています。
　 点状物質Ｄの10秒間以上の時空間移動（ 空間の単位も秒です ）は、 その間に絶え間なく新たなガラス板に存在位置を記して、 順にガラス板を重ねていき、 それを真上から眺めた２次元平面における、 原点を一端とする線分で示されます。

　 以上の４つの点状物質の移動を観察しているのが太郎君であるとします。 太郎君の観察する太郎君の慣性系は２次元直交時空間座標系です。 では、 太郎君対して 速さ で空間を直線的に移動している花子さんが、 太郎君の慣性系を観察するとどのようになるでしょうか。 花子さんが太郎君の慣性系を観察するということは、 太郎君の立場に立って４つの点状物質の移動を観察するということです。（ 花子さんが太郎君の立場に立つと、 点状物質Ａは移動して、 点状物質Ｄは静止します。）そのためは、 ローレンツ変換をすればいいのです。 すると、 ４本の線分は元のままですが、 座標系が太郎君の観察する太郎君の慣性系とは異なる２次元斜交時空間座標系になります。 点状物質Ｃの移動を表す線分上の点の時間軸からの距離と空間軸からの距離は等しくなっています。

　 点状物質Ａの移動は、 ローレンツ変換により、 空間移動が０秒間より大きくなり、 時間移動が10秒間より大きくなって、 時空間移動は10秒間より大きくなっています。 点状物質Ｂの移動は、 ローレンツ変換により、 空間移動が10秒間より大きくなり、 時間移動が０秒間より大きくなって、 時空間移動は10秒間より大きくなっています。 点状物質Ｃの移動は、 ローレンツ変換により、 空間移動が10秒間未満になり、 時間移動が10秒間未満になって、 時空間移動は減少しています。 点状物質Ｄの移動は、 ローレンツ変換により、 空間移動が０秒間になり、 時間移動が10秒間未満になって、 時空間移動は10秒間未満に減少しています。

　 ローレンツ変換は、 元々、 光子の移動について２つの慣性系で比較することから求められたものですから、 ローレンツ変換の前後で、 空間や時間がどう変化するのかを調べるためには、 点状物質Ｃの移動に着目すべきでしょう。 ローレンツ変換によって、 点状物質Ｃの移動空間も移動空間も減少しています。 したがって、「 ローレンツ変換とは、 時間を減らし、 空間を減らす変換である。」、 つまり、「 逆ローレンツ変換とは、 時間を増やし、 空間を増やす変換である。」と結論づけて、「 移動している慣性系では静止しているときに比べて、 万物の活動がスローになっており、 万物は慣性系の移動方向に伸展している。」と言い切りたいところですが、 定説では、「 移動している物質は活動がスローになっており、 移動方向に収縮している。」のです。 これは、 定説が、 時間に関しては点状物質Ｄに注目し、 空間に関しては点状物質Ｂに注目しているためです。 ここが腑に落ちない所です。