
※ スリップ率が正の数なら滑っていて、負の数なら空回りしています。
円O: 半径 1 自転も公転もしません。
円A: 半径 r 円Oに接触し続けて、自転しながら公転します。
スリップ率 = 0 % のとき、円Aが1回公転したときには、円Aは (1+r) / r 回 自転しています。なぜなら、円Aの円周上の点も円Aの移動距離( 物質の移動距離は、重心の移動距離です。)と同じ距離 2π(1+r) 移動しており、それを円Aの円周の長さ 2πr で割れば自転数が求まるからです。
スリップ率 = 0 % のとき、かつ、 r=1 のとき、 円Aが1回公転したときには、円Aは2回自転しています。
口と底の直径の比率が 2:1 の紙コップが2つあります。同じ大きさです。机の上に普通に置いた紙コップの右隣にもう1つの紙コップを逆さにして置き、両方を線で接触させます。そして、左の紙コップを時計回りに右の紙コップを反時計回りに同時に1回転させます。このとき、 ① 紙コップの高さの半分の所で水平に切った断面での2つの円の運動、 ② 紙コップの一番低い所で水平に切った断面での2つの円の運動、 ③ 紙コップの一番高い所で水平に切った断面での2つの円の運動、この3つについて考えてみましょう。
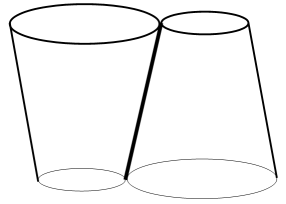
右の紙コップの立場に立って左の紙コップの運動を見てみましょう。すると、左の紙コップがじっとしている右の紙コップの回りを1回公転したときに2回自転していることになります。これは ① ~ ③ に共通しています。したがって、右の円の半径に対する左の円の半径の比を r とすると、 ① ~ ③ の左の円の運動のスリップ率はすべて次のようになります。( 1回公転する時間が単位時間であると考えるとよい。)
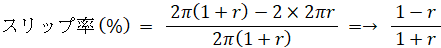
※ 左のコップの円の相対的移動距離は、円の中心の移動距離です。
① の場合: r = 1 を代入して、 スリップ率 = 0 %
② の場合: r = 1/2 を代入して、 スリップ率 = 100/3 % : 「 滑り優位のスリップ 」
③ の場合: r = 2 を代入して、 スリップ率 = -100/3 % : 「 空回り優位のスリップ 」
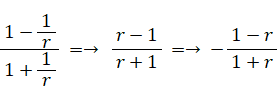
 剛体力学 へ戻る
剛体力学 へ戻る