【 問 題 1 】
-
思考簡単化のため、大きさが g m/s-2 の重力加速度の一様な重力場において、空気抗力や摩擦力が全く存在しないものとする。
半径 r m の扇形をした崖がある。崖の頂上から水平方向に初速 v0 m/s で質量 m kg の玉を打ち出す。
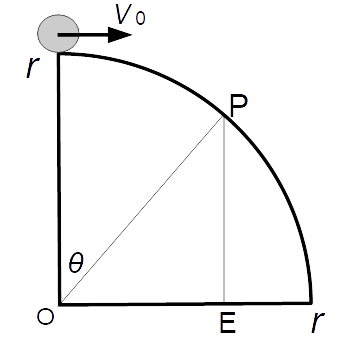
-
(1) 崖に接触することなく放物線を描いて落下させるために最低限必要な v0 の値を求めよ。
(2) v0 = 0 のとき、点Pで玉は崖を離れて落下する。PEの長さを求めよ。
(1)
-
半径 r m 、速さ v0 m/s の等速円運動を考える。この運動を作るのは大きさが m v02 / r N の向心力である。この問題の場合、移動開始時には大きさが mg N の向心力が働くので、次の等式を立てる。
mg = m v02 / r
よって、 v0 = root ( rg )
v0 がこの値よりも小さければ、玉は崖に束縛されて一次的にも崖からの抗力を受けながら落下することになる。逆にこの値より大きければ、玉は崖に束縛されないで、崖に接触することなく放物線を描いて落下する。
-
点Pにおける玉の速さを v m/s とする。点Pにおける玉に働く力を図示すると、次のようになる。
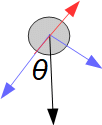
黒色の矢印、つまり、玉に作用する重力、は青色の矢印に分解されて無くなったとしてほしい。
また、実際は、赤色の矢印、つまり、壁が玉に作用する抗力、の大きさは0である。
点Pは、今まで存在していた崖による玉への抗力が無くなる瞬間の玉の位置になる。この時の向心力の大きさは m v2 / r N である。また、向心力の大きさは mg cos θ N でもある。したがって次の式が成り立つ。
m v2 / r = mg cos θ
よって、 v2 = rg cos θ ・・・ ①
また、エネルギー保存法則より次の式が成り立つ。
mg r ( 1-cos θ ) = 1/2 × m v2
よって、 v2 = 2rg ( 1-cos θ ) ・・・ ②
① と ② より、
cos θ = 2×(1-cos θ )
よって、 cos θ = 2/3
cos θ = PE / r だから、
PE / r = 2/3
よって、 PE = 2/3 × r
-
重りの質量 m kg 、紐の長さ r m の単振り子がある。重りが真下の位置にある時に水平方向に速さ v0 m/s で打ち出す。重りが真上に来るまでは紐に束縛されて円運動をし、その後に紐の束縛から自由になって移動するための v0 の範囲を求めよ。
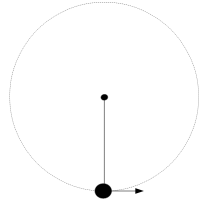
-
重りが真上に来た時に重りの速さが0になるときの v0 の値が、重りが真上に来るまで紐に束縛されて紐の張力を受けながら円運動をするために最低限必要な v0 の値になる。この場合、エネルギー保存法則より、次の式が成り立つ。
1/2 × m v02 = 2×mg r
よって、 v0 = 2 root ( rg )
次に、初速 v0 = 2 root ( rg ) よりも大きな力で玉を打ち出したとき、玉が真上に来たときの玉の速さを v m/s とする。ここで、半径 r m 、速さ v m/s の等速円運動を考える。この運動を作るのは大きさが m v2 / r N の向心力である。この問題の場合、玉が真上に来たとき、それも紐の張力が作用しない場合には、大きさが mg N の向心力が働くので、次の等式を立てる。
mg = m v2 / r
よって、 v2 = rg ・・・ ①
また、エネルギー保存法則より、次の式が成り立つ。
1/2 × m v02 = 1/2 × m v2 + 2×mg r
よって、 v02 = v2 + 4 rg ・・・ ②
① を ② に代入して、
v02 = 5 rg
よって、 v0 = root ( 5 rg )
v0 が root ( 5 rg ) 以下ならば、たとえ玉が真上に来て水平方向に速度を持っていたとしても、それから後は玉は紐の張力を受けないことになる、つまり、紐に束縛されずに移動することになる。
というわけで、答えは、 2 root ( rg ) m/s 以上 root ( 5 rg ) m/s 以下 である。
 力学 へ戻る
力学 へ戻る