力学的束縛（ 力学的拘束 ）の原因になるものを束縛力と言います。
　束縛力には 垂直抗力 と 伸び縮みしない紐の張力 があります。
　垂直抗力は接触する２物体の間に現れます。張力は繋がった物質と紐の間に現れます。
　摩擦力 や 空気抗力 や 浮力 も束縛力であるように思えます。
　しかし、これらの力は原則的には束縛力の定義からは外されています。
　お互いに束縛をする２物質間の相対的移動に関して仕事をしない力であることが、束縛力の必要条件だからです。
　この必要条件より、束縛力の方向には、２物体のそれぞれの加速度は等しくなっています。

　下線の部分は、例えば、摩擦のない世界で床の上に置かれた傾斜台の上にそっと置かれた物質が滑り落ちるような２物体の運動を解析するときに重宝されます。

　　　
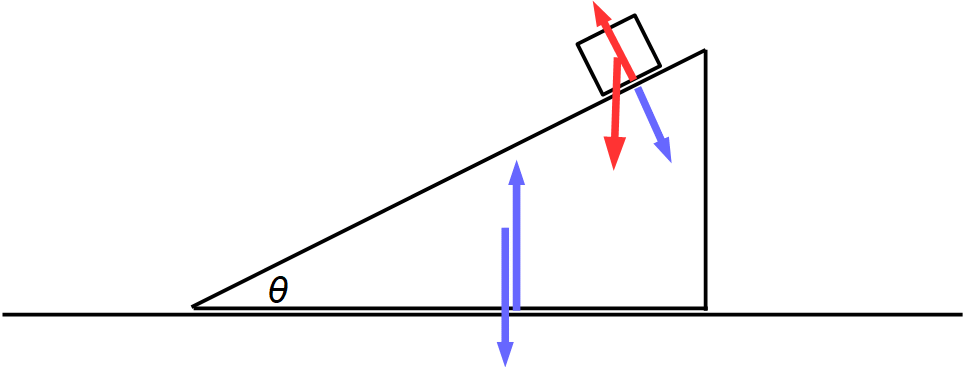
　　　　　　　※　単位は省略します。上方向を y 軸方向、右方向を x 軸方向とします。
　　　　　　　　　　　斜面台の質量を M とします。
　　　　　　　　　　　物質の質量を m とします。
　　　　　　　　　　　重力加速度を g とします。
　　　　　　　　　　　斜面台が物質に及ぼす垂直抗力の大きさを N とします。
　　　　　　　　　　　物質の加速度の x 方向の大きさを a_x とします。
　　　　　　　　　　　物質の加速度の y 方向の大きさを a_y とします。
　　　　　　　　　　　斜面台の加速度の x 方向の大きさを A_x とします。

　上図に描いたような一定の力が作用するので、２物体はそれぞれ等加速度直線運動をします。その方向は次のようになります。

　　　

　　　　　　　　　　　　　　　　

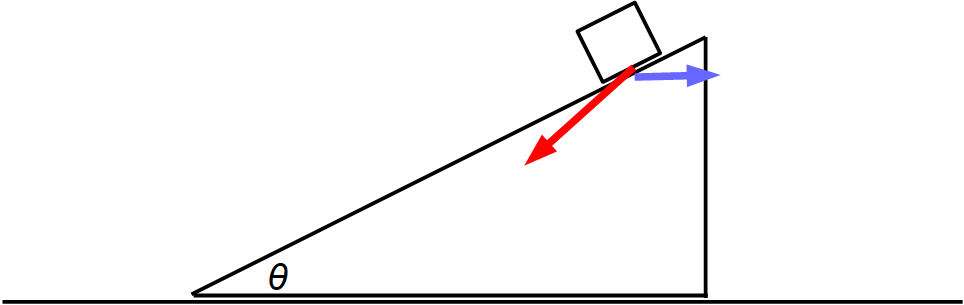
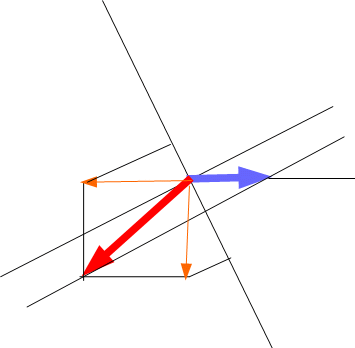
　束縛力の方向には２物体のそれぞれの加速度は等しくなっていますので、次の式が成り立ちます。
　　　−a_x sin θ ＋ a_y cos θ　＝　A_x sin θ
　　　よって、
　　　　　　a_y ＝ ( a_x ＋ A_x ) tan θ　　・・・ �@
この式は「束縛条件」を表す式です。

　加速度を求める式たちです。いわゆる運動方程式です。
　　　−a_x　＝　1 / m　×　( −N sin θ )　　・・・ �A
　　　−a_y　＝　1 / m　×　( −m g ＋ N cos θ )　　・・・ �B
　　　　A_x　＝　1 / M　×　N sin θ　　・・・ �C

　この後、４つの連立方程式を解いて、a_x ，a_y ，A_x ，N　が求まります。それぞれ次のようになります。
　　　a_x　＝　M g sin θ cos θ　÷　( M ＋ m sin²θ )
　　　a_y　＝　( m ＋ M ) g sin θ cos θ　÷　( M ＋ m sin²θ )
　　　A_x　＝　m g sin θ cos θ　÷　( M ＋ m sin²θ )
　　　N　＝　m M g cos θ　÷　( M ＋ m sin²θ )