音楽と物理学 へ戻る（１） ２つの音で作られる協和音 と ３つの音で作られる協和音
-
ド の音よりも高くて、 振動数比が １：２ になっている音は、 １オクターブ高いド の音です。 振動数比が簡単な整数比ですから、 心地良い和音（ 協和音 ）です。
ド の音よりも高くて、 振動数比が ２：３ になっている音は、 ソ の 音です。 振動数比が簡単な整数比ですから、 協和音です。
２つの音で作られる和音には、 ヒトに共通する気分明暗のイメージがありませんが、 ３つ以上の音で作られる和音は、 そのイメージを持っています。 そのスタンダードな分類方法が、 長調（ メジャー ）と 短調（ マイナー ）です。
長調（ メジャー ）か 短調（ マイナー ）かは、 ２：３ の振動数比関係を持つ２つの音 （ 長調では ド と ソ になり、 短調では ラ と ミ になります ） の間に持ってくる音によって決まります。
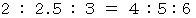になるような音を入れると、 長調になります。
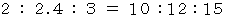になるような音を入れると、 短調になります。-
純正調における長調の音階の振動数比は次のようになります。
ド ： レ ： ミ ： フｧ ： ソ ： ラ ： シ ： ド
＝ 24 ： 27 ： 30 ： 32 ： 36 ： 40 ： 45 ： 48
ラ ： シ ： ド ： レ ： ミ ： フｧ ： ソ ： ラ
＝ 40 ： 45 ： 48 ： 54 ： 60 ： 64 ： 72 ： 80
ラ ： シ ： ド ： レ ： ミ ： フｧ ： ソ ： ラ
＝ 120 ： 135 ： 144 ： 160 ： 180 ： 192 ： 216 ： 240
＝→ 40 ： 45 ： 48 ： 53. 333 ： 60 ： 64 ： 72 ： 80
純正調の長調 ：
Ⅰの和音 ドミソ の振動数比 ： 24 ： 30 ： 36 ＝→ ４ ： ５ ： ６
Ⅳの和音 ファラド の振動数比 ： 32 ： 40 ： 48 ＝→ ４ ： ５ ： ６
Ⅴの和音 ソシレ の振動数比 ： 36 ： 45 ： 54 ＝→ ４ ： ５ ： ６
純正調の短調 ：
Ⅰの和音 ラドミ の振動数比 ： 120 ： 144 ： 180 ＝→ 10 ： 12 ： 15
Ⅳの和音 レファラ の振動数比 ： 160 ： 192 ： 240 ＝→ 10 ： 12 ： 15
Ⅴの和音 ミソシ の振動数比 ： 180 ： 216 ： 270 ＝→ 10 ： 12 ： 15
-
純正調 と 平均律 との違いは、 アナログ と デジタル の違いのようなものでしょうか。 現在、 電気通信分野では、 アナログからデジタル化が進行していますが、 音楽も純正調から平均律へと移行してきたものと思います。 したがって、 ドレミファソラシドの音階のルーツに迫るのには、 平均律音階よりも純正調音階に注目すべきではないかと考えます。
ある音が１つ与えられたとします。 この音を ド とします。 これから、 ド との和音を使って、 いろんな音を作っていきましょう。
ド よりも高くて、 振動数比が １：２ になる音。 これは １オクターブ高いド の音です。
ド よりも高くて、 振動数比が ２：３ になる音。 これは ソ の音です。
ド よりも低くて、 振動数比が ２：３ になる音。 これは ファ の音です。
ソ よりも高くて、 振動数比が ２：３ になる音。 これは レ の音です。
ド と ソ の間にあり、 振動数比が ４：５：６ になるような音。 これは ミ の音です。
ファ と ド の間にあり、 振動数比が ４：５：６ になるような音。 これは ラ の音です。
ソ と レ の間にあり、 振動数比が ４：５：６ になるような音。 これは シ の音です。
これらの音を低い順に並べて、 振動数比を表します。
ファ ： ラ ： ド ： ミ ： ソ ： シ ： ド ： レ
＝ 16 ： 20 ： 24 ： 30 ： 36 : 45 ： 48 ： 54
ファ ラ
32 40
16 ： 20 ： 24 ： 30 ： 36 ： 45 ： 48 ： 54
27レこれらの音を、 低い順に並べ替えると、 次のようになります。
ド ： レ ： ミ ： フｧ ： ソ ： ラ ： シ ： ド
＝ 24 ： 27 ： 30 ： 32 ： 36 ： 40 ： 45 ： 48
① ２：３ （ ド：ソ ）
② 12：18
③ ８：12：18：27 （ ファ：ド：ソ：レ ）
④ 16：24：36：54
⑤ 16：20：24：30：36：45：54 （ ファ：ラ：ド：ミ：ソ：シ：レ ）
ファラド、ドミソ、ソシレ は 振動数比 ４：５：６ の和音である。
⑥ 24：27：30：32：36：40：45
16と20は２倍にし、54は半分にして、小さい順に並べた。
② 12：18
③ ８：12：18：27 （ ファ：ド：ソ：レ ）
④ 16：24：36：54
⑤ 16：20：24：30：36：45：54 （ ファ：ラ：ド：ミ：ソ：シ：レ ）
ファラド、ドミソ、ソシレ は 振動数比 ４：５：６ の和音である。
⑥ 24：27：30：32：36：40：45
16と20は２倍にし、54は半分にして、小さい順に並べた。
① １：２ （ ド：ド ）
② １：1.5：２ ← ドとドの間にソを入れた。
③ ２：３：４ （ ド：ソ：ド ）
④ ２：2.5：３：４ ← ドとソの間にミを入れた。
⑤ ４：５：６：８ （ ド：ミ：ソ：ド ）
⑥ 24：30：36：48
⑦ 16：20：24：30：36：45：48：54
ドが一番高くなる ４：５：６ の和音を加え、ソが一番低くなる ４：５：６ の和音を加えた。
振動数 ４：５：６ の和音は、楽しい明るい気分を表すというか、そういった気分を作る。
⑧ 24：27：30：32：36：40：45：48
16と20は２倍にし、54は半分にして、小さい順に並べた。
② １：1.5：２ ← ドとドの間にソを入れた。
③ ２：３：４ （ ド：ソ：ド ）
④ ２：2.5：３：４ ← ドとソの間にミを入れた。
⑤ ４：５：６：８ （ ド：ミ：ソ：ド ）
⑥ 24：30：36：48
⑦ 16：20：24：30：36：45：48：54
ドが一番高くなる ４：５：６ の和音を加え、ソが一番低くなる ４：５：６ の和音を加えた。
振動数 ４：５：６ の和音は、楽しい明るい気分を表すというか、そういった気分を作る。
⑧ 24：27：30：32：36：40：45：48
16と20は２倍にし、54は半分にして、小さい順に並べた。
-
純正調では、 ハ長調 から イ短調 に転調した時には、 レの音 （ 音名ではＤの音 ） を少し下げてやらなければならないし、 純正調のハ長調に調音された音たちは、 曲がニ長調に転調するやいなや、 それぞれの音を若干上げたり下げたしなければならなくなります。 例えば、 音名がＥの音 （ 音階名では、 ハ長調ではミの音、 二長調ではレの音 ） は、 バイオリンで弾くとき、 曲がハ長調からニ長調に転調したら若干高くしなければなりません。 テレビドラマ 「 のだめカンタービレ 」 で一躍有名になったベートベンの交響曲第７番、 その第２楽章の冒頭のように頻回な和音的転調がある場合には特に神経を使います。
-
純正調
平均律
ド
1.000
1.000
レ
1.125
1.122
ミ
1.250
1.260
ファ
1.333
1.335
ソ
1.500
1.498
ラ
1.667
1.682
シ
1.875
1.888
ﾄﾞ
2.000
2.000
以上のことは鍵盤楽器では不可能です。 そこで、 鍵盤楽器を用いて自由に転調できるようにするための方法が１９世紀半ばに確立しました。 それが平均律音階です。 言ってみれば、 純正調音階は階段一段一段の高低比 （ 高低差ではありません ） がまちまちなので、 これを同じ高低比にしたのが平均律なのです。
平均律での音階の作り方はこうです。 純正調ができたときの基本は、 ド ： ソ ： ド ＝ ２ ： ３ ： ４ でしたので、 これに従います。 つまり、 基準になるド の音よりも高くて振動数比が ２：３ になる音を帰納法的な順番に作っていくのです。 するとまず、 ソ の音ができ、 次にその ソ の１.５倍の振動数を持ったレ の音ができ、 その次に、 その レ の１.５倍の振動数を持った ラ の音ができ、 その次の次に、 ・ ・ ・ ・ ・ というふにして、 これを１２回続けると、 最後は元の ド よりも ７オクターブ高いド の音になります。 この間にできた音は、 １２個です。そしてそれらの音を基本の ド の音の振動数の １倍 ～ ２倍 の間になるように、 振動数を
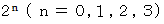で割ります。 そして、 それら１２個の音を、 時計の周りに配置します、 ド の音が１２時の位置になるようにして、 それから音の低い順に、 時計の １時、 ２時、 ３時、 ・ ・ ・ に配置します。 そうすると、 ドレミファソラシド は図のような配置になります。 それぞれが持つ振動数は、 純正調の振動数と若干異なります。 （ 同じ物もあります。） かといって、 平均律が出来上がっているわけでもありません。 そこで、 隣どおしの音 （ 半音違いの音 ） の振動数比がすべて 
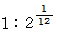になるように均等化するのです。
この図を 「 ソラシ時計 」 と言う人がいるようですが、 私は 「 ミファソらせん階段 」 のほうがいいのではないかと思います。 また、 数字に順番に半音ずつ上がる音名を対応させると、 シャープが１個付くたびに、 主音が７度上がって、 何調になったのかが早わかりします。 ＮＨＫ高校講座で秋山仁先生が、 Ⅰ度、Ⅳ度、Ⅴ度の和音の ３つの音を結んでできる３角形が同じ形をしていることを紹介されています。
最後に、 ド の音の振動数を
としたとき、 純正調 と 平均律 でそれぞれの音階の振動数比がいくらになっているのかを小数で表してみます。
-
純正調 長音階 の レシピ （ 協和音の簡単な整数で表される振動数比より ）
ふぁ
ど
そ
れ
ら
2/3
1
3/2
9/4
ら
み
し
2/3×5/4
5/4
3/2×5/4
ふぁ
ら
ど
み
そ
し
れ
2/3
5/6
1
5/4
3/2
15/8
9/4
16
20
24
30
36
45
54
32
40
24
30
36
45
27
ど
れ
み
ふぁ
そ
ら
し
ど
24
27
30
32
36
40
45
48
ど
そ
れ
ら2/3
1
3/2
9/4
ら
み
し
2/3×5/4
5/4
3/2×5/4ふぁ
ら
ど
み
そ
し
れ2/3
5/6
1
5/4
3/2
15/8
9/416
20
24
30
36
45
5432
40
24
30
36
45
27ど
れ
み
ふぁ
そ
ら
し
ど24
27
30
32
36
40
45
48純正調 短音階 の レシピ （ 協和音の簡単な整数で表される振動数比より ）
そ
れ
ら
み
し
2/3
1
3/2
9/4
ふぁ
ど
そ
2/3×6/5
6/5
3/2×6/5
れ
ふぁ
ら
ど
み
そ
し
2/3
4/5
1
6/5
3/2
9/5
9/4
40
48
60
72
90
108
135
80
96
120
144
180
216
270
160
192
120
144
180
216
135
ら
し
ど
れ
み
ふぁ
そ
ら
120
135
144
160
180
192
216
240
れ
ら
み
し
2/3
1
3/2
9/4
ふぁ
ど
そ
2/3×6/5
6/5
3/2×6/5
れ
ふぁ
ら
ど
み
そ
し2/3
4/5
1
6/5
3/2
9/5
9/4
40
48
60
72
90
108
135
80
96
120
144
180
216
270160
192
120
144
180
216
135
ら
し
ど
れ
み
ふぁ
そ
ら120
135
144
160
180
192
216
240