変数が多数あるとき、それらの関係性を知るために個別に見るのではなく、それぞれの相関係数を要素とする対角行列を作成して、それを表現行列とする演算子テンソルの、垂直に交わる２つの固有ベクトルを求めて、独立する新たな２つの変数を求めると、データーの織りなす縦横の関係性が見えやすくなることがあります。これは、「 多変数解析 」のうちの「 主成分分析 」と言われます。

　次のような８人の生徒の３教科の試験結果のデーターがあります。

	生徒Ａ	生徒Ｂ	生徒Ｃ	生徒Ｄ	生徒Ｅ	生徒Ｆ	生徒Ｇ	生徒Ｈ
英語	84点	66点	82点	93点	72点	70点	81点	64点
数学	67点	94点	86点	88点	72点	51点	80点	73点
国語	79点	70点	70点	90点	64点	58点	83点	60点

　　　　　英語の平均点 ：　76.5 点
　　　　　数学の平均点 ：　76.4 点
　　　　　国語の平均点 ：　71.8 点
　　　　　英語の分散 ：　88.5
　　　　　数学の分散 ：　164.2
　　　　　国語の分散 ：　113.2
　　　　　　　　＊ 分散とは平均からのへだたりの２乗の平均
　　　　　英語と数学の共分散 ：　29.1
　　　　　数学と国語の共分散 ：　70.0
　　　　　国語と英語の共分散 ：　85.8
　　　　　　　　＊ 共分散とは２つのへだたりを掛け合せたたものの平均
　　　　　　　　　　　　　　※ 参照： 大学生のための数学 ＞ 統計学 ＞ 共分散
　　　　　英語と数学の相関係数 ：
　　　　　　　　　
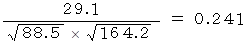
　　　　　数学と国語の相関係数 ：
　　　　　　　　　
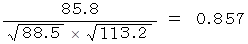
　　　　　国語と英語の相関係数 ：
　　　　　　　　　

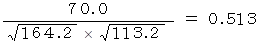
各科目間の相関係数の一覧表を作ります。

	英語	数学	国語
英語	１	0.241	0.857
数学	0.241	１	0.513
国語	0.857	0.513	１

相関係数の別の求め方：
　　
　　標準偏差 ² ＝ 分散
　　各データーの値を偏差比に変換することを「標準化」と言います。

	生徒Ａ	生徒Ｂ	生徒Ｃ	生徒Ｄ	生徒Ｅ	生徒Ｆ	生徒Ｇ	生徒Ｈ
英語	0.797	−1.116	0.584	1.753	−0.478	−0.691	0.478	−1.328
数学	−0.259	0.474	0.265	0.320	−0.121	−0.701	0.099	−0.094
国語	0.677	−0.169	−0.169	1.711	−0.733	−1.297	1.053	−1.109

　　　　　　　　　　英語の平均点 ：　０ 点
　　　　　　　　　　数学の平均点 ：　０ 点
　　　　　　　　　　国語の平均点 ：　０ 点
　　　　　　　　　　英語の分散 ：　１
　　　　　　　　　　数学の分散 ：　１
　　　　　　　　　　国語の分散 ：　１
　　　　　　　　　　英語と数学の共分散 ＝ 0.241　　← 英語と数学の相関係数
　　　　　　　　　　数学と国語の共分散 ＝ 0.513　　← 数学と国語の相関係数
　　　　　　　　　　国語と英語の共分散 ＝ 0.856　　← 国語と英語の相関係数

相関行列 ：
　　　

　　　Maxima などの固有値と固有ベクトルを求めるアプリケーションソフトを用いて、
　　　　　固有値： 2.117　＆　大きさ１の固有ベクトル（ 0.605, 0.437, 0.666 ）
　　　　　固有値： 0.790　＆　大きさ１の固有ベクトル（ −0.488, 0.864, −0.124 ）
　　　　　固有値： 0.093　＆　大きさ１の固有ベクトル（ −0.629, −0.250, 0.736 ）

　　　第１主成分：
　　　　　　Ｚ₁ ＝ 0.605 × ( 英語の点数 ) ＋ 0.437 × ( 数学の点数 ) ＋ 0.666 × ( 国語の点数 )
　　　第２主成分：
　　　　　　Ｚ₂ ＝ −0.488 × ( 英語の点数 ) ＋ 0.864 × ( 数学の点数 ) − 0.124 × ( 国語の点数 )
　　　　　　　　　　　＊ 各人の点数ベクトル と 固有ベクトル の内積を求めている。
　　　　　　　　　　　　　　　　→ 各人の総合的な点数配置における固有ベクトル方向の原点からの隔たりが求められる。
　　　　　　　　　　　＊ 各人の偏差比ベクトル と 固有ベクトル の内積を求めても可。

　　　第１主成分の寄与度： 2.117 ÷ 3 ≒→ 70.6 %
　　　第２主成分の寄与度： 0.790 ÷ 3 ≒→ 26.3 %
　　　この２つを合せた寄与度： 96.9 % ＞ 90 %

　第１主成分 や 第２主成分 というのは、いわば加重平均によって加工され新たに作り出された変数です。対角行列の固有ベクトルは直交しますので、第１主成分と第２主成分は関係性のない独立した変数であるということです。
　第１主成分の式を見ると、若干の加重はあるもののその程度は少ないので、第１主成分は３教科の総合点に近いものであることがわかります。第１主成分は「主成分分析的加工」をしたときに新しい変数の分散が最大になるものです。
　第２主成分の式を見ると、英語と国語は点数が良いほど低く評価されて、数学は点数が良いほど高く評価されていることがわかります。したがって、第２主成分は理系が得意な人を過大評価した加工点であることがわかります。というわけで、文系が比較的得意で理系が比較的苦手な人 と 理系が比較的得意で文系が比較的苦手な人 との区別が付きやすくなったことが分かります。次の表をご覧ください。

	生徒Ａ	生徒Ｂ	生徒Ｃ	生徒Ｄ	生徒Ｅ	生徒Ｆ	生徒Ｇ	生徒Ｈ	平均
Ｚ1	132.7	127.6	133.8	154.7	117.6	103.3	139.2	110.6	127.4
Ｚ2	7.1	40.3	25.6	19.5	19.1	2.7	19.3	24.4	19.8

　この表のＺ₂ の値より、生徒Ｂや生徒Ｈは理系が比較的得意で、生徒Ａや生徒Ｆは文系が比較的得意であることが分かります。