【 問 題 1 】
-
質量 m1 kg の物質A と 質量 m2 kg の物質B が存在し、大きさ f N の引力によってお互いが中点に向かって加速度運動をしている。
このとき、物質Bの物質Aに対する相対加速度を求めよ。
-
物質Aの加速度の大きさ: f / m1 m/s2
物質Bの加速度の大きさ: f / m2 m/s2
答えは、
f / m2 + f / m1 m/s2
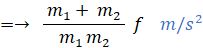
これが答えであるが、運動方程式を意識するためにさらに式を変形する。
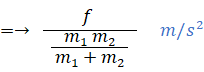
ここで、次のように置く。
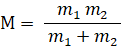
2つの物質があり、2つの物質間の作用・反作用の関係になる力だけで2つの物質が運動しているとき、一方の物質から見た他方の物質の運動方程式は、その物質の質量が上記の質量であるとして次のように表せばいい。
a = f / M
このように「換算質量 ( M ) 」という概念を作ると、「相対運動方程式」という概念もでき上がるのである。
ということは、質量は相対なものであるということである。よく考えてみればこれは全く不思議なことではない。質量はエネルギーであり、運動エネルギーや位置エネルギーは物質と観察者との関係で変化する相対なものだからだ。
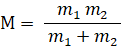
2つの物質があり、2つの物質間の作用・反作用の関係になる力だけで2つの物質が運動しているとき、一方の物質から見た他方の物質の運動方程式は、その物質の質量が上記の質量であるとして次のように表せばいい。
a = f / M
このように「換算質量 ( M ) 」という概念を作ると、「相対運動方程式」という概念もでき上がるのである。
ということは、質量は相対なものであるということである。よく考えてみればこれは全く不思議なことではない。質量はエネルギーであり、運動エネルギーや位置エネルギーは物質と観察者との関係で変化する相対なものだからだ。
【 問 題 2 】
-
摩擦のない机の上に台となる質量 m1 kg の直方体の物質Aが置いてある。その台の上を質量 m2 kg の直方体の物質Bを初速 v m/s で滑らす。物質Aと物質Bの間の動摩擦係数を μ 、重力加速度を g m/s2 として、物質Bが物質Aの上を滑る距離を求めよ。

-
水平方向には、物質Aと物質Bの間の作用・反作用の力としての摩擦力のみしか働かないので、 換算質量 ( M ) を利用することができる。
物質Bが物質Aの上を滑る距離を L m とすると、物質Aから見た物質Bの仕事による運動エネルギー変化の式は次のようになる。
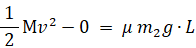
※ 右辺の摩擦力は垂直方向の外力なので M ではなく m2 になっていることに注意!
よって、
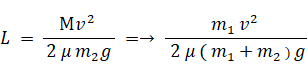
-
質量 1 kg 速さ 6 m/s の物質A と 質量 2 kg 速さ 4 m/s の物質B とがお互いに反対方向から来て正面衝突をした。物質Aと物質Bの反発係数は 0.5 である。2つの物質が接触して撃力が作用する僅かな時間に平均 2000 N の大きさの 衝突重量力( 筆者の造語 )が働いていた。その僅かな時間とは何秒間だったのか?

-
水平方向には、物質Aと物質Bの間の作用・反作用のみしか働かないので、換算質量 ( M ) を利用することができる。M = 2/3 である。
求める時間を t s とすると、力積が運動量の変化量を表すので、 次の式が成り立つ。
M × 0.5×( 6+4 ) + M × ( 6+4 ) = 2000 × t
よって、 t = 1/200
というわけで、 答えは 0.005 秒間 である。
-
等速直線運動をしている2つの物質の衝突においては、運動量保存の法則が成り立っている。したがって、 重心速度: ( 1×6 − 2×4 ) / ( 1+2 ) =→ −2/3 は一定である。
重心と並走している観察者からすると、
最初の物質Aの速度は 20/3 m/s 最初の物質Bの速度は −10/3 m/s
衝突後の物質Aの速度は −10/3 m/s 衝突後の物質Bの速度は 5/3 m/s
求める時間を t s とすると、力積が運動量の変化量を表すので、 次の式が成り立つ。
1×10/3 + 1×20/3 = 2000 × t または、
2×5/3 + 2×10/3 = 2000 × t
よって、 t = 1/200
というわけで、 答えは 0.005 秒間 である。
 力学 へ戻る
力学 へ戻る