「 固有時間は、 それぞれの物質が持っている絶対的な時間であり、 それは座標変換で不変である。」と、 アインシュタインの相対性理論は言います。 いろんな速さで移動している時計がたくさんあるとき、 観察者が１自転する時間をそれぞれの時計で計った結果は、 様々な値を取ります。 この場合、 時計の数だけ「 固有時間 」があり、 そのうち観察者に対して静止している時計で計った時間を「 その観察者の慣性系の固有時間 」とは言わずに「 時間 」と言います。 また、 ある時計で計った時間を「 その時計の慣性系の固有時間 」と言います。
　　　　　　　　　　　　 慣性系とは、 等速直線運動をしている ある範囲の空間のことです。

　　　　　

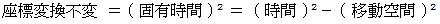
　 ローレンツ変換は、 マクスウェルの方程式が座標変換で不変になるような座標変換を求めて、 ローレンツが発見したものですが、 アインシュタインは、 固有時間が座標変換で不変になるような変換を求めて、 同じローレンツ変換を導きました。「 ローレンツ変換は、 移動する物質を観察している観察者Ａ から その物質と並走しながら観察している観察者Ｂ への座標変換である。」と アインシュタインは言います。 彼の「 自由自在なローレンツ変換 」のイメージは、 １個の被観察物質 と いろんな速さで移動しているたくさんの観察者たちです。 ちなみに私の「 自由自在なローレンツ変換 」のイメージは、 １人の観察者といろんな速さで移動しているたくさんの同一規格の被観察物質たちです。


　「 観察者が移動している時計を用いて計った時間 」のことを「 その観察者にとってのその時計の慣性系の相対時間 」と 私は言っています。 つまり、 アインシュタインの相対性理論の言う「 その時計の慣性系の固有時間 」という言葉を否定して、「 その観察者にとってのその時計の慣性系の相対時間 」という言葉に置き換えているのが、 私です。「 相対時間 」は、 私の造語です。 また、 私は、 アインシュタインの相対性理論の言う相対的な存在としての「 時間 」という概念を否定して、「 絶対時間 」という言葉を使っています。

　　　　　

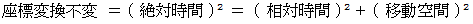
　 私は、「 移動する物質を観察している観察者Ａ から その物質と並走しながら観察している観察者Ｂ への座標変換は、 ローレンツ変換ではなく、 次のような回転である。」と 考えています。 回転とは、 直交座標系から他の直交座標系への座標変換の一種です。 私の「 自由自在な回転 」のイメージは、 １個の被観察物質 と いろんな速さで移動しているたくさんの観察者たちです。


反時計方向に ラジアン回転させる座標変換 ：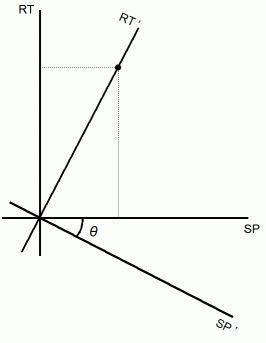

　　　　　　

　　　

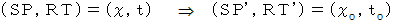
　　　基底変換式 ：
　　　　　　　

　　　座標変換式 ：
　　　　　　　

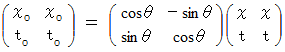
　　　上図の点の座標変換 ：
　　　　　　　
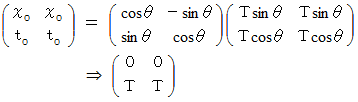
　　　　　　　したがって、
　　　　　　　　　　　

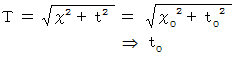
　 私の考えでは、 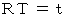は「 相対時間 」で、 は「 絶対時間 」ですが、 アインシュタインの相対性理論では、 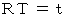は「 時間 」で、 は「 固有時間 」です。

　 ローレンツ変換は、 直交座標系から斜交座標系の変換ですが、 時間を虚数とすると、 反時計方向に ラジアン回転させる座標変換 に変えることができます。 なぜなら、 次のような式になるからです。
　　　　　
しかし、 虚数時間を認めない私は、 このやり方には反対しています。


　「 相対時間 」の概念が、 私（ ばいおりん ）の主張の核心です。 固有時間が ０ のときは、 私の主張はアインシュタインの相対性理論と同じになります。 固有時間が ０ のときとは、 光などの電磁波の伝達です。 アインシュタインは、「 光の伝達に関しては固有時間は座標変換しても ０ のまんまで不変だから、 一般の物質の移動も固有時間は座標変換しても不変なんだろう。」と仮定して、 今の相対性理論を構築したのです。 そのためにいろんな矛盾 （ 定説はそれをパラドックスと言っています。） が起こっており、 そのために相対性理論は魅力的であり、 アインシュタインはみんなから愛されているのです。