【 問 題 】

無重力下での実験です。質量 m kg の重りの付いたひもをストローの中をくぐらせて下端を手で持って固定します。
固定されたストローから出ているひもの長さは重りまで 2r m です。
重りを速さ v m/s で等速円運動させます。
(1) ひもの下端を固定している手にはひもからどんな大きさの引っ張る力を受けますか?
ひもをゆっくりと引っ張って少しずつストローから出ているひもの重りまでの長さを短くしていき r m にしました。
(2) 重りの速さはいくらになりますか?
(3) 手が重りに対してした仕事はいくらですか?
-
(1) 遠心力の大きさで、 mv2 / 2r (N)
(2) 系に与えた外力は回転軸に平行な力だけなので、「 質点の角運動量保存の法則 」より、質点の運動量モーメントは一定になる したがって、重りの速さを V m/s とすると、
rmV = 2rmv
よって、 V = 2v
答えは、 2v (m/s)
(3) 重りの持つ運動エネルギーの増加分は、
1/2 × m × 4v2 − 1/2 × m × v2 =→ 3/2 × m × v2
手が重りに対してした仕事は重りの持つ運動エネルギーの増加分に等しいので、
答えは、 3/2 × m × v2 (J)
( 確かめ )
最初から x m ひもを引っ張ったときの重りの速さを V m/s とすると、
質点の運動量モーメントは一定なので、
( 2r− x ) mV = 2rmv
よって、 V = 2rv / (2r− x )
手に加わる力は、
mV2 / (2r− x ) =→ 4r2mv2 / (2r− x )3
したがって、手が重りに対してした仕事は、
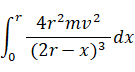
ここで、2r− x = t と置くと、
d x = −dt x : 0 → r ⇒ t: 2r → r
よって、
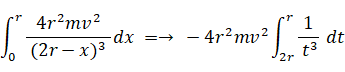
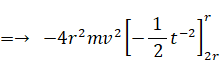
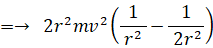
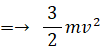
 力学 へ戻る
力学 へ戻る