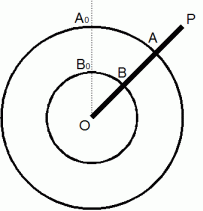
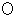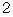
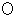
同じ中心 とする外円と内円の半径の長さは、 それぞれ 、 になっています。 線分 が１２時方向から出発して時計回りに角速度 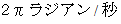で回転します。 線分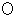 の外円および内円の交点を、 それぞれ Ａ、 Ｂ とします。 時刻 ０秒 から 時刻 １秒 の時間において、 時刻 秒における Ａ の Ａ_０ からの道のり と Ｂ の Ｂ_０ からの道のり を、 それぞれ 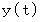、 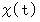とします。 すると、 次の式たちが成り立ちます。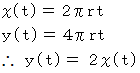
　　　　　


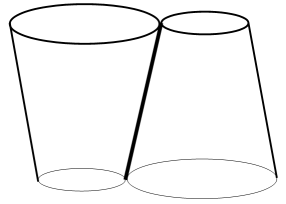
　 同じ大きさの紙コップを２つ用意してください。 一方は普通に机の上に置き、 一方は伏せて机の上に置きます。 ２つの紙コップを接触させます。 すると接触した部分は机に対して垂直ではない線分になっています。 ２つの紙コップを接触させたまま、 同じ角速度の大きさで２つのコップを回転させてください。 ただし回転方向は２つのコップで逆向きにします。 紙コップの高さのちょうど真ん中の接点は、 スリップ無しの「 歯数無限大歯車様回転（私による造語）」になっていますが、 それから遠のくに従ってスリップの割合が多くなる「 スリップ回転（私による造語）」になっています。 回転半径が小さい方が滑っていて、回転半径が大きい方が空回りしていて、２つの紙コップはスリップし合っています。

　　　　　　


　 車軸となる同じ長さの棒を２つ用意してください。 歯数が １：２ になっている噛み合う歯車を２個用意してください。 それぞれの歯車を３次元コピーして、 合計４個の歯車にしてください。 大小の歯車を車軸で繋げて、 段違い車輪を２個作ってください。 お互いに大小の歯車をかみ合わせて、 車軸が平行になるようにしてください。 一方の車軸を回転させようとしてみてください。 回転しないはずです。

　　　　　　　　　


【 問 題 】

半径 1 m の車輪が氷の上を滑って移動しているが、同時に車輪は滑りを止める方向に回転している。
滑り初めてから止まるまでに車輪は ８ π m 移動し、かつ、２回転した。
車輪の滑る速さの平均 は 転がる速さの平均 の何倍だったか？

【 解 答 】

車輪が 8 π m 移動する間に車輪は仮想的に −2 × 2 π m 転がったと考えることができる。
したがって、車輪が 8 π m 移動する間に車輪は仮想的に 8 π＋２×２π m 滑ったと考えることができる。
したがって、12 π ÷ 4 π ＝→ 3 で、車輪の滑る速さの平均 は 転がる速さの平均 の３倍であったことが分かる。

　参考： 大学生のための数学 ＞ その他の数学 ＞ アリストテレスの輪のパラドックス