（１） 斜面を滑り落ちる時間

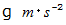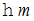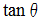　 大きさが の一様な重力場の中の、 摩擦のない世界です。 高さが 、 傾き（ ）が 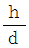の坂道を、 初速 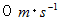で最高点から最低点まで、 質量 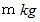の物質が滑り落ちます。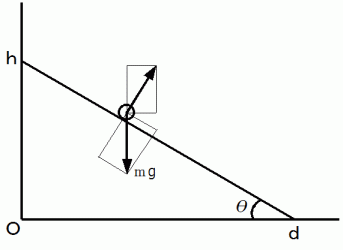

　　　　

　 この間、 この物質に働く重力と抗力で、 その大きさはそれぞれ次のようになります。
　　　　
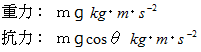
したがって、 重力と抗力はずっと一定であり、 したがって物質は等加速度運動をします。


　滑り落ちる時間を、 鉛直方向の運動方程式を作ってから求める。

　 鉛直方向の力の大きさ
　　　　　
　 鉛直方向の加速度の大きさを 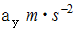とすると、 鉛直方向の運動方程式は次のようになります。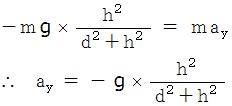
　　　　
　 鉛直方向の速度の大きさを 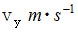、 運動を開始してからの時間を とすると、 等加速度運動ですから、 次の式が成り立ちます。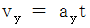
　　　　
ここで、 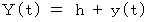とすると、 次のようになります。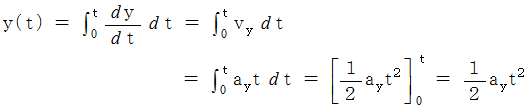
　　　　
　　　　
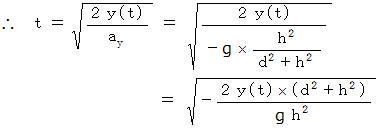
　のとき、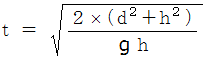
　　　　


　滑り落ちる時間を、 斜面方向の力積から求める。

初速 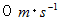で、 一定の力による力積は、 次の式が成り立ちます。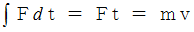
　　　　
エネルギー保存法則より、 最低点での速さに関しては、 次の式が成り立ちます。
　　　　
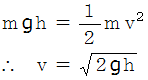
斜面方向に働く力の大きさ ：　
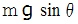
したがって力積は次のようになります。
　　　　

（２） 最速降下軌道

　　　　

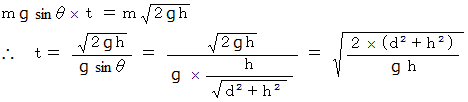
　 大きさが 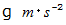の一様な重力場の中の、 摩擦のない世界です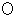。 点 と 点 との間に好きなように軌道を作って、 重力のみに任せて、 質量 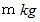の物質を 点 から 点 まで最短時間で移動させるには、 どんな軌道を作ったらいいでしょうか？
ただし、 点 の位置を　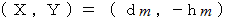　とします。

　第１感は、 直線軌道です。 最短距離だからです。 この軌道では、 転がる時間は次のようになります。
　　　　

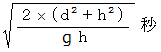
　 しかし、 正解は直線軌道ではありません。 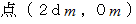と 点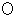 を結んで 点 を底とするサイクロイド曲線が正解とのことです。 蒲鉾型のサイクロイド曲線は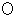、 点 から 点 に向かうにつれて傾斜が次第に緩やかになってきます。 どうしてサイクロイド軌道が最速降下軌道になるのかの証明は難しくて、 今の私には太刀打ちできそうもありません。