（ 問 題 ）

　　　　　

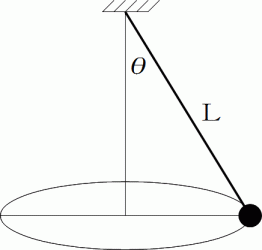
　 紐の長さ 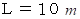、　重りの質量 　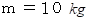の円錐振り子がある。
　 振り子の鉛直角 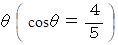　の所で、 重りを円錐振り子の円軌道の接線方向に
初速 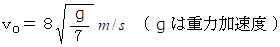で打ち出した。
　 すると、 次第に鉛直角を増し、 鉛直角 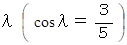　の所で安定した水平な等速円運動の軌道に入った。

　 そのときの重りの速さ （ ） を求めよ。

（ 解 答 その１ ）

　 重りが打ち出されたのは円錐振り子の中心軸から６ｍ離れた所からである。 安定した水平な等速円運動の軌道の半径は８ｍであり、 これは重りが打ち出された所よりも２ｍ上方である。

力学的エネルギー保存の法則より、
　　　　　

（ 解 答 その２ ）

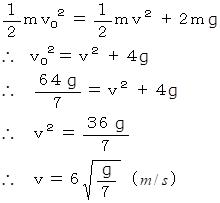
　 重りが打ち出されたのは円錐振り子の中心軸から６ｍ離れた所からである。 安定した水平な等速円運動の軌道の半径は８ｍであり、 これは重りが打ち出された所よりも２ｍ上方である。

　 重りに作用する力は重力と紐の張力であるが、 これらを合成すると重りの水平な円運動の中心を常に向く向心力になる。 重りの水平な円運動の中心を原点とする（ 原点は徐々に上方移動する ）重りの位置ベクトルは常に向心力と反対向きなので、「 質点の周回移動における運動量モーメント不変の法則（ 私によるネーミングで、 一般には 角運動量保存の法則 と言われている ）」が成り立つ。
したがって、
　　　　

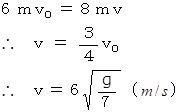
　「 角運動量保存の法則 」については、　大学生のための物理学 ＞ 剛体力学 ＞ 剛体の回転運動　の中の（２） の と をご覧ください。