ドローンを飛ばして、ある空点（ x₀ , y₀ ）（ ※ x₀ も y₀ も 0 より大きい実数 ）に静止させます。座標系の原点からそのドローンを撃ち落とすべく砲丸を繰り返し発射させます。砲丸の質量は 0.1 kg で、初速は 10 m/s です。打ち上げ角度を θ（ 0 ＜ θ ≦ 90 ）度とします。空気抵抗は無いものとします。ドローンが絶対に撃ち落されないためには、どの範囲にドローンを固定させればいいのかを考えてみましょう。

運動方程式：
　　d ² x / d t ² ＝ 0
　　d ² y / d t ² ＝ − g （ g は重力加速度 ）
したがって、
　　d x / d t ＝ 10 cos θ
　　d y / d t ＝ −g t ＋ 10 sin θ
したがって、
　　x ＝ 10 t cos θ
　　y ＝ −0.5 g t ² ＋ 10 t sin θ

ドローンが存在する空点が砲丸の軌道上にあるとすると、
　　x₀ ＝ 10 t cos θ　　・・・ �@
　　y₀ ＝ −0.5 g t ² ＋ 10 t sin θ　　・・・ �A

�@ より、 t ＝ 0.1 x₀ / cos θ　これを �A に代入して、
　　y₀ ＝ −0.005 g x₀ ² / cos ² θ ＋ x₀ tan θ
よって、
　　y₀ ＝ −0.005 g x₀ ² ( tan ² θ ＋ 1 ) ＋ x₀ tan θ
よって、
　　0.005 g x₀ ² tan ² θ − x₀ tan θ ＋ ( y₀ ＋ 0.005 g x₀ ² ) ＝ 0　　・・・ �B

　0 ＜ tan θ ≦ ＋∞　だから、�B の式が成立しないための必要十分条件は、�B が tan θ について実数解を持たないことである。そのための必要十分条件は、次の２次方程式の判別式が成り立つことである。
　　x₀ ² − 0.02 g x₀ ² × ( y₀ ＋ 0.005 g x₀ ² ) ＜ 0
よって、
　　1 − 0.02 g × ( y₀ ＋ 0.005 g x₀ ² ) ＜ 0
よって、
　　y₀ ＞ −0.005 g x₀ ² ＋ 50 / g

これが求めるドローンの配置の範囲になります。
g ＝ 9.8 とすると、上記の式はおよそ次のようになります。
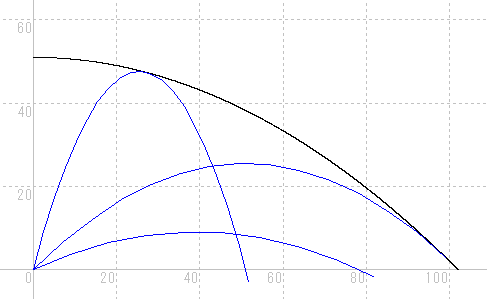
　　y₀ ＞ −0.0049 x₀ ² ＋ 51
y₀ ＝ −0.0049 x₀ ² ＋ 51　の式で言えば、
　　x₀ ＝ 0　のときは、 y₀ ＝ 51　となり、
　　y₀ ＝ 0　のときは、およそ x₀ ＝ 102　となります。