（１） 写像と座標変換の違い

　 写像では変換前と変換後の２つのベクトルが存在しますが、 座標変換で存在するのは１つのベクトルだけです。 写像はベクトルの変換ですが、 座標変換はベクトルの表現方法の変換です。 言い換えると、 写像は１人の観察者におけるベクトルの変換ですが、 座標変換は２人の観察者におけるベクトルのイメージの変換です。
　 座標変換では、 変換前と変換後に２つの基底が存在します。 基底とは、 単位ベクトルたちの順列です。 座標変換の本質は基底の変換です。 写像はベクトルの変換ですが、 座標変換は基底の変換です。

（２）　相対性理論の矛盾

　 相対性理論によりますと、 被観察物質に対して静止している第０観察者の基底 と 移動している第１観察者の基底 とは異なります。 相対性理論の基本となるローレンツ変換は、 第１観察者の座標系 から 第０観察者の座標系 への変換であるとします。 第０観察者の基底を第０基底とし、 第１観察者の基底を第１基底とします。 第０基底は、 第１基底に比べてその大きさが異なることはもちろんですが、 基底を構成する単位ベクトルたちの一部が直交していません。 移動とは相対的な現象ですから、 Ａさんに対してＢさんが移動しているときには、 Ｂさんに対してＡさんも移動しています。 したがって、 Ｂさんを被観察物質とするときは、 ＡさんからＢさんへの座標変換は、 第１基底から第０基底への変換であり、 かつ、 ＢさんからＡさんへの座標変換は、 第０基底から第１基底への変換です。 また、 Ａさんを被観察物質とするときは、 ＢさんからＡさんへの座標変換は、 第１基底から第０基底への変換であり、 かつ、 ＡさんからＢさんへの座標変換は、 第０基底から第１基底への変換です。 これは矛盾です。 なぜ矛盾しているのか解るためには、 ＡさんとＢさんを被観察物質とし、ＡさんとＢさんが同じ速さで移動しているとする新たな観察者Ｃを登場させたときのことをイメージすればいいでしょう。 その上で、 座標変換によって被観察物質の活動スピード（ 老化速度など ） が変化するという相対性理論の定理を思い出せばいいのです。


　 この矛盾を解決するためには、 次のような考え方をするしかありません。
　「 第１基底は第１観察者の座標系の現実的な基底なのですが、 第０基底は、 第０観察者の座標系の現実的な基底ではなくて、 第１観察者がイメージする第０観察者の座標系の基底なのです。」


　 第１観察者の座標系の現実的な基底 と 第１観察者がイメージする第０観察者の座標系の基底。 それらに基づく２つの座標表現を比べて、 それを、 第１観察者の座標系と第０観察者の座標系とを比べているのだと勘違いしているのが、 現在の相対性理論です。 その上、 現在の相対性理論は、 第１観察者の座標系の現実的な基底に基づく座標表現 と 第１観察者がイメージする第０観察者の座標系の基底に基づく座標表現 とを比べるときに、「 ４次元時空間の構成要素としての時間（ いわゆる固有時間 ）」を等しくさせてから「 ４次元時空間距離としての時間（ いわゆる時間 ）」の大きさを比べますので、 座標変換によって時間の大きさが変化することになります。 だったら逆に、「 ４次元時空間距離としての時間（ いわゆる時間 ）」を等しくさせてから「 ４次元時空間の構成要素としての時間（ 相対時間 ）」の大きさを比べるというのはいかがでしょうか。

　　コメント ：
　　　　　アインシュタインの特殊相対性理論の基本となる式は次のようになっています。
　　　　　　　　
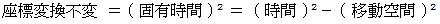
　　　　これは、 ( 時間 )^２ ＝ ( 移動空間 )^２ ＋ ( 固有時間 )^２　と書くことができます。
　　　　さらに、 座標変換不変 ＝ ( 時間 )^２ ＝ ( 移動空間 )^２ ＋ ( 移動時間 )^２　とするの
　　　　はいかかでしょうか？　アインシュタインは「 ４次元時空間の構成要素としての時間 」
　　　　と「 ４次元時空間距離としての時間 」との取り違えをしているように思うからです。