( 問 題 )
-
質量 0.1 kg の球を水平方向に撃ち出して速さ 9.8 m/s で反発係数 0.5 の板に垂直に衝突させたときの衝撃 と 質量 0.1 kg の球を高さ 4.9 m の所から自然落下させて反発係数 0.5 の板に垂直に衝突させたときの衝撃 とどちらが大きいか?
重力加速度( g ) = 9.8 m/s2 として考えてください。
( 誤 解 その1 )
-
質量 0.1 kg の球を水平方向に撃ち出して速さ 9.8 m/s で反発係数 1 の板に垂直に衝突させたときの球の運動エネルギーは 1/2 × 0.1 × 9.82 ≒→ 4.8 J である。
一方、質量 0.1 kg の球を高さ 4.9 m の所から自然落下させたときの衝突時の運動エネルギーは 0.1 × 9.8 × 4.9 ≒→ 4.8 J である。
したがって、両者の衝撃の程度は等しい。
( 誤 解 その2 )
-
質量 0.1 kg の球を水平方向に撃ち出して速さ 9.8 m/s で反発係数 1 の板に垂直に衝突させたときの力積は 質量 × 入射速度の大きさ ×( 1+ 反発係数 ) =→ 0.1 × 9.8 × 1.5 =→ 1.47 Ns である。
質量 0.1 kg の球を高さ 4.9 m の所から自然落下させたときの運動方程式:
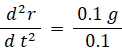
両辺を t で積分して、
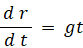
両辺をさらに t で積分して、
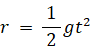
r = 4.9 をこの式に代入すると、t = 1 となる。 t = 1 のときの速さは 9.8 m/s である。
したがって、この場合も力積は 1.47 Ns であり、両者の衝撃は等しいように思われるが、実は違って、落下による衝突の場合は、運動の威力による力積が作用している間にさらに球の重量力が作用するので、力積は 1.47 Ns よりも大きくなるのである。したがって、後者の方が衝撃の程度が大きいのである。
( 解 説 )
-
誤 解 その2 は一見正しいように思われますが、間違いです。なぜなら、2つの誤解とも衝撃の程度を計る物差しが違うからです。衝撃の程度を計る物差しは、運動エネルギー でも 運動量( その変化量を力積と言う )でもありません。なぜなら、衝突の時の球が非常に大きな運動エネルギーを持っていて大きな 撃力 を与えたとしても、板や球の材質が非常に弾力性があって( バネならばバネ係数が低くて )衝突後に時間をかけて接触して徐々に球が減速した場合には「衝撃が吸収されて」衝撃の程度が小さくなるのです。
どうも衝撃の程度を計る物差しは、球が衝突を開始してから急停止するまでの時間のようですが違います。衝撃の程度を計る物差しは、球の急停止の減速度( マイナスの加速度 )の平均値に球の質量をかけたもの( 衝突重量力 )です。 たとえば、質量 0.1 kg の球が速さ 9.8 m/s から 0 m/s になるのに 0.1 s かかったときの衝突重量力は、 0.1 × ( 9.8 ÷ 0.1 ) ≒→ 9.8 N になります。衝突重量力はベクトルです。
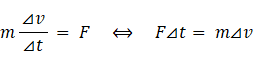
「重量力」は私が勝手に作った言葉です。そして「衝突重量力」も私が勝手に作った概念です。「静止重量力」は、重力位置エネルギーが変化しない物質が落下を防いでくれるものに作用する力のことで、その大きさは、その物質の質量に重力加速度をかけたもの( 単位は N )になります。「衝突重量力」は、前述したように、衝突時の急停止の減速度「衝突瞬間減速度」の大きさに質量をかけたものになります。追突が上から下への方向の場合の 衝撃の程度は「衝突重量力」に「静止重量力」を加えたもので表現しなければなりません。
「衝突重量力」という概念は、完全弾性衝突の力積を考える上でも必要になってきます。
※ 参考: 力学 > 完全弾性衝突における力積
-
① 質量 0.01 kg、直径 0.01 m の球を、一辺の長さが 6 m の立方体Aの面に垂直に、速さ 30 m/s でぶつけたところ、食い込んでいき当たってから 0.1 s 後に 1.5 m の深さで止まりました。その間の球の加速度は一定の負の数でした。( 完全非弾性衝突 )
② 質量 0.01 kg、直径 0.01 m の球を、一辺の長さが 6 m の立方体Bの面に垂直に、速さ 30 m/s でぶつけたところ、食い込んでいき当たってから 0.2 s 後に 3 m の深さで止まりました。その間の球の加速度は一定の負の数でした。( 完全非弾性衝突 )
(1) ① と ② それぞれについて、球が当たってから止まるまでの加速度を求めなさい。
(2) ① と ② それぞれについて、球が当たってから止まるまでの衝突重量力を求めなさい。
(3) ① と ② それぞれについて、球が当たってから止まるまでの力積を求めなさい。
-
(1)
-
① -30 m/s ÷ 0.1 s =→ -300 m/s2
② -30 m/s ÷ 0.2 s =→ -150 m/s2
-
① 0.01 kg × 300 m/s2 =→ 3 N
② 0.01 kg × 150 m/s2 =→ 1.5 N
-
① 3 N × 0.1 s =→ 0.3 Ns
② 1.5 N × 0.2 s =→ 0.3 Ns
-
衝突重量力は、2つの物質の間の衝突直後の短い時間内に作用する撃力の平均値です。衝突重量力に撃力が作用する時間をかけると力積になります。力積は運動量の変化に等しくなっています。撃力が作用する時間は、完全非弾性衝突の場合は、2つの物質が衝突してから2つの物質の移動速度が等しくなるまでの時間で、それ以外の場合は、2つの物質が衝突してから接触が無くなるまでの時間です。
 力学 へ戻る
力学 へ戻る