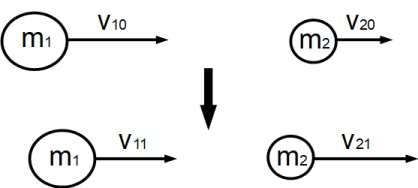
物質Ａ：　質量 m₁ kg　　衝突前の速さ v₁₀ m/s　　衝突後の速さ v₁₁ m/s
　　　　　物質Ｂ：　質量 m₂ kg　　衝突前の速さ v₂₀ m/s　　衝突後の速さ v₂₁ m/s
　　　　　　　　　　　　※ 右向きの速度を ＋ で、左向きの速度を − で表します。

　　
　　　　　　　
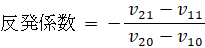
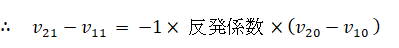
　　反発係数 ＝ ０ とは 完全非弾性衝突を表し、反発係数 ＝ １ とは 完全弾性衝突を表します。


　話は変わりますが、「衝突の前後で２つの物質の系の運動量の総和は変化しない。」という真実があります。
反発係数が ０〜１の範囲のどんな値を取ろうともです。
これを式で表すと次のようになります。
　　　m₁ v₁₀ ＋ m₂ v₂₀　＝　m₁ v₁₁ ＋ m₂ v₂₁　　・・・・ �@
以上は「運動量保存の法則」と言われています。

衝突における運動量の変化の式は次の２つです。
　　　m₁ v₁₁ − m₁ v₁₀　＝　力積₁ 　　・・・・ �A
　　　m₂ v₂₁ − m₂ v₂₀　＝　力積₂ 　　・・・・ �B
　　　　　　　　　※ 力積とは、ベクトルの仲間であり、力を時間で積分したものである。
　　　　　　　　　※ 右向きの力積を ＋ で、左向きの力積を − で表します。
　　　　　　　　　※ 力積₁ ＋ 力積₂ ＝ ０　（ 作用反作用の法則より ）
�A と �B を辺々加えると �@ が得られます。

「運動量保存の法則」は、�A や �B の式において、力積 ＝ ０ のときに次の式が成り立つということを言っているのではありません。
　　　m₁ v₁₁ ＝ m₁ v₁₀
　　　m₂ v₂₁ ＝ m₂ v₂₀

ちなみに、「慣性の法則」は、 力 ＝ ０ のときは、運動方程式： a ＝ F / m　だから　a ＝ 0　になるということを言ってます。



【 問 題 】

質量 1 kg 速さ 6 m/s の物質Ａ と 質量 2 kg 速さ 4 m/s の物質Ｂ とが お互いに反対方向から移動して来て正面衝突をした。
この２つの物質間の反発係数は 0.5 である。
衝突後の２つの物質の速度をそれぞれに求めよ。

【 解 答 】

物質Ａの移動方向を正とする。
衝突後の物質Ａの速さを v₁₁ m/s とし、衝突後の物質Ｂの速さを v₂₁ m/s とする。

反発係数の公式より：
　　v₂₁ − v₁₁ ＝ −0.5 × ( v₂₀ − v₁₀ )
　　よって、
　　　　v₂₁ − v₁₁ ＝ −0.5 × ( 2×(−4) − 1×6 )
　　つまり、
　　　　v₂₁ − v₁₁ ＝ 5　　・・・ �@

運動量保存の法則：
　　1×6 ＋ 2×(−4)　＝　1×v₁₁ ＋ 2×v₂₁
　　よって、
　　　　v₁₁ ＋ 2 v₂₁ ＝ −2　　・・・ �A

�@ と �A の連立方程式を解くと、
　　　v₁₁ ＝ −4　　　v₂₁ ＝ 1

したがって答えは、次のようになる。
　　物質Ａは衝突前と反対方向に速さ 4 m/s で移動する。
　　物質Ｂは衝突前と反対方向に速さ 1 m/s で移動する。