赤色細胞が消滅増加したときに、赤色細胞が誕生する確率は1/2であり、かつ、青色細胞が誕生する確率は1/2であるので、次のようになります。
元の赤色細胞が消滅して2つの赤色細胞が誕生する確率は 1/4
元の赤色細胞が消滅して2つの青色細胞が誕生する確率は 1/4
元の赤色細胞が消滅して赤色細胞と青色細胞が1つずつ誕生する確率は 1/2
赤色細胞が誕生する事象を A とし、青色細胞が誕生する事象を B とすると、上記の確率分布は次の式を用いて表すことができます。
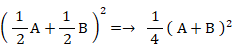
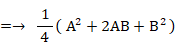
青色細胞が消滅増加ときに、青色細胞が誕生する確率は1/2であり、かつ、赤色細胞が誕生する確率は1/2であるので、次のようになります。
元の青色細胞が消滅して2つの青色細胞が誕生する確率は 1/4
元の青色細胞が消滅して2つの赤色細胞が誕生する確率は 1/4
元の青色細胞が消滅して青色細胞と赤色細胞が1つずつ誕生する確率は 1/2
「1個の赤色細胞が消滅増加を2回繰り返して4個の細胞になったとき、青色細胞と赤色細胞の個数の組み合わせの確率分布を求めよ。」という問題の答えは、次の式を用いて求めることができます。
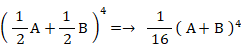
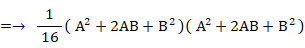
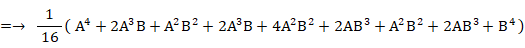
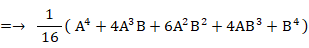
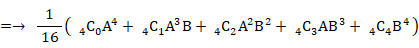
上の式は二項定理です。 ⇒ 参照:確率 > 確率の二項分布 ( 独立試行の反復確率 )
したがって、答えは次のようになります。
4個とも赤色細胞の確率は 1/16
4個とも青色細胞の確率は 1/16
1個だけが青色細胞の確率は 1/4
1個だけが赤色細胞の確率は 1/4
赤色細胞と青色細胞が2個ずつの確率は 3/8
※ 参照:その他の数学 > 遺伝の計算
 確率 へ戻る
確率 へ戻る