考えやすくするために、 実際の４次元時空間を、 １次元空間と１次元時間の２次元時空間とします。 また、 光の速さを とする単位系を用います。 Ａ君とＢ君は相対的等速直線運動をしています。 ２人がちょうど重なった時（ 思考実験につき衝突しないものとします ）に、 ２つのレーザー光が放たれました。 一つは、 Ｂ君のＡ君に対する移動方向に、 もう一つは、 Ａ君のＢ君に対する移動方向に。 ２人にとって、 その後の３つの物質（ Ａ君、Ｂ君、光 ）の時空間における移動を考えてみましょう。 そして、 の時間後の３つの物質の位置ベクトルを見てみましょう。

　　　　　　　　　　　Ａ君とＢ君が相対的等速直線運動をしている時点で、 Ａ君にとっては
　　　　　　　　　　　Ｂ君は自分よりもゆっくりと老化しており、 Ｂ君にとってはＡ君は自分よ
　　　　　　　　　　　りもゆっくりと老化している、 というのが定説になっています。
　　　　　　　　　　　　これに対して、 私は、 老化のスピードは２人とも同じであると主張して
　　　　　　　　　　　います。

：　Ａ君の座標系
　　　直交座標系 ：
　　　　　Ｂ君： 等速直線運動
　　　　　　　　　　　　 の時間経過、　 の速さ
　　　　　　　　　　　　最終位置ベクトル　
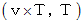
　　　　　Ａ君： 等速直線運動
　　　　　　　　　　　　 の時間経過、　 の速さ
　　　　　　　　　　　　最終位置ベクトル　
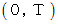
　　　　　 光： 等速直線運動
　　　　　　　　　　　　 の時間経過、　 の速さ
　　　　　　　　　　　　最終位置ベクトル　


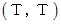
：　Ｂ君の座標系
　　　直交座標系 ：
　　　　　Ａ君： 等速直線運動
　　　　　　　　　　　　 の時間経過、　 の速さ
　　　　　　　　　　　　最終位置ベクトル　
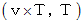
　　　　　Ｂ君： 等速直線運動
　　　　　　　　　　　　 の時間経過、　 の速さ
　　　　　　　　　　　　最終位置ベクトル　
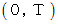
　　　　　 光： 等速直線運動
　　　　　　　　　　　　 の時間経過、　 の速さ
　　　　　　　　　　　　最終位置ベクトル　


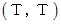
：　Ａ君が観察するＢ君の座標系
　　　斜交座標系 ：
　　　　　Ｂ君： 等速直線運動
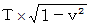　　　　　　　　　　　　　の時間経過、　 の速さ
　　　　　　　　　　　　最終位置ベクトル　
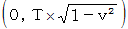
　　　　　Ａ君： 等速直線運動
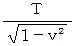　　　　　　　　　　　　　の時間経過、　 の速さ
　　　　　　　　　　　　最終位置ベクトル　
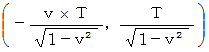
　　　　　 光： 等速直線運動
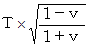　　　　　　　　　　　　　の時間経過、　 の速さ
　　　　　　　　　　　　最終位置ベクトル　


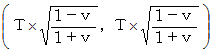
：　Ｂ君が観察するＡ君の座標系
　　　斜交座標系 ：
　　　　　Ａ君： 等速直線運動
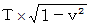　　　　　　　　　　　　　の時間経過、　 の速さ
　　　　　　　　　　　　最終位置ベクトル　
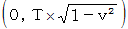
　　　　　Ｂ君： 等速直線運動
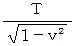　　　　　　　　　　　　　の時間経過、　 の速さ
　　　　　　　　　　　　最終位置ベクトル　
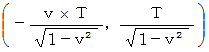
　　　　　 光： 等速直線運動
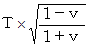　　　　　　　　　　　　　の時間経過、　 の速さ
　　　　　　　　　　　　最終位置ベクトル　


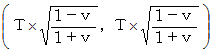
　 ローレンツ変換前の と ローレンツ変換後の 、 または、 ローレンツ変換前の と ローレンツ変換後の において、 ３つの物質の移動の様子は同じですが、 その移動の表現方法が異なってきます。 なぜなら、 ２つの座標系で２軸の交差角度が異なる上に、 １目盛りの長さが異なるからです。 ローレンツ変換では、 変換前には、 ２つの座標軸は直交していますが、 変換後には 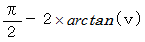の交差になり、 また、 １目盛りの長さは、 変換後には 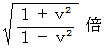に拡張します。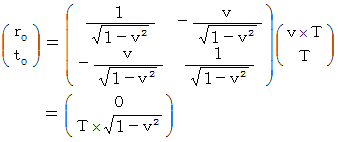

　　　
　　　
　　　


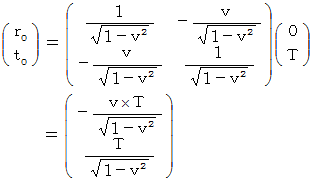
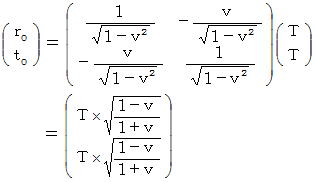
　 ローレンツ変換前の と ローレンツ変換後の 、 または、 ローレンツ変換前の と ローレンツ変換後の とを比較して、 座標系によって時間や空間が収縮したり拡張したりすると言っているのが今日の定説の特殊相対性理論です。 それを私は、「 ニュートン力学的な観察方法 から 相対論的な観察方法 への翻訳の前後での無意味な比較 」と言っており、「 相対論において比較をするのなら、 ローレンツ変換後の と ローレンツ変換後の とを比較すべきであり、 そうすれば、 特殊相対性理論においても、 時間や空間が収縮したり拡張したりすることはない。」と主張していて、 特殊相対性理論の本質は次のようなものであると主張しています。
　　　　移動の相対性
　　　　相対性原理
　　　　相対時間を含む４次元時空間内の万物の移動の速さの普遍性
　　　　第３者的な観察の否定
　　　　空間速度の非ニュートン力学的合成
　　　　質量の波動的概念
　　　　波動の時空間合成・分解原理
　　　　電場と磁場の４次元時空間解釈
　　　　運動量とエネルギーと質量の等価性